by Rebecca Torrey
Associate Professor of Math
Brandeis University
Traditional Grading Sends the Wrong Message
For many years I taught Calculus with a traditional structure, in which the students’ grades were mostly determined by a few high-stakes exams (a final and a couple of midterms). In my classes, I would tell my students:
- How important it was to practice regularly;
- To carefully review their exams and the solutions;
- That it’s ok to get things wrong and learn from their mistakes;
- That the idea that we can improve through practice applies in math just as it would in anything else they want to learn.
But the structure of my class was giving them a very different message. The structure told them:
- You only really need to study three times during the semester: right before the midterms and the final;
- Don’t bother reviewing your work since you will rarely, if ever, get tested on those same problems again;
- You can only do well in the class if you get all the problems (including the very hardest) right on the first try.
It gets worse. Based on the compelling work of Claude Steele, we started reading out a statement before our exams that said:
- “This test has not shown any gender or racial differences in performance or mathematical ability.”
This statement was carefully crafted to be technically true — the test had never been given before, so it couldn’t have shown any biases. We adopted this with the best of intentions: research had shown that making a declaration like this could, like a self-fulfilling prophecy, help to reduce stereotype threat. I hope it worked, at least for some students. But in practice I suspect our tests actually sent a message more like:
- Somehow you have to divine our expectations about how to properly write your solutions out, which (for whatever reason) you’re much more likely to do successfully if your gender and racial identities match those traditionally overrepresented in math.
There were other ways my pedagogical structure was undermining my own messages. I told my students:
- We care primarily about your understanding of the math and communication of it.
But our structure was saying:
- If you can write down some vaguely-related words and symbols, you can probably rack up enough points to pass the class.
Here’s another one. We told students:
- There’s no cap on the number of students who can get an A in this class.
This was technically true. We didn’t stick to a strict curve. But, with many years of experience, we wrote exams for which we could predict the distribution of scores with remarkable accuracy and then set the grades around the median.
You get the idea. The structure of the course was undermining pretty much all of my pedagogical ideals.
What did we do about it? We instituted Outcomes-Based Assessment (also known as Mastery Grading, Standards-Based Grading, or Specifications-Based Grading). There are many different versions of this, but the basic idea is that you have a list of the ideas, skills, techniques, etc., that you want your students to learn over the course of the semester (“content outcomes”, or “outcomes” for short, in our terminology). You have some way for them to demonstrate mastery of those skills. The grading is credit/no-credit (either they have demonstrated mastery or not). And the students can try multiple times to demonstrate mastery of each outcome.
Our Version of Outcomes-Based Assessment
Our initial version of this was copied pretty much wholesale from Jeff Ford of Gustavus Adolphus College. We’ve tweaked it a bit around the edges since then, but it still has the same basic format. I’d also like to give an official shout-out to Eric Hanson, currently at the Norwegian University of Science and Technology, who, as a graduate student at Brandeis, was instrumental in converting our first class (Precalculus).
Here are the components.
Content Outcomes:
Our outcomes are fairly fine-grained. Here are a few sample outcomes for our Differential Calculus class:
- Determine information about a function from the graph of its derivative (or vice versa).
- Find and classify the extrema of a function.
- Solve an optimization word problem using the methods of Calculus
It was important to us that our students also be able to apply their knowledge on problems they haven’t seen before, so we include a few outcomes like:
- Solve a challenging problem that combines different skills and/or presents material from Chapters 2-3 + Pre-Reqs in a different way.
We also decided that there were some things that were so fundamental that a student shouldn’t be able to pass the class without mastering them, so we split these out into a category of “Fundamental Outcomes”. Some of these are prerequisites, like factoring polynomials or evaluating trig functions, and some are key elements of the class, like finding the equation of a tangent line or calculating derivatives.
Assessments:
We test our students every Friday. On each test, we have a problem corresponding to every outcome we’ve covered so far in the course. Students have to earn credit on two different Fridays to master a particular outcome. After this, they no longer have to do those problems.
Our bar for earning credit is B+/A- level work. If it’s on the border, we ask ourselves questions like, “do they really understand the idea and have they communicated that?” and “do I think they need to spend some more time on this?”. These are the questions that really determine the cutoff
Illustration by Simon Huynh
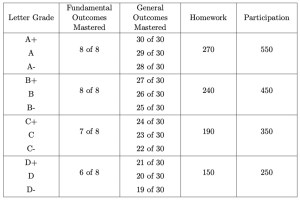
Students’ grades are then determined by how many of the outcomes they master. Here’s the grade breakdown from our Differential Calculus class:
Students need to earn the minimum points for all categories across a given row to earn the letter grade in the left column.
In practice, the grades are pretty much entirely determined by the General Outcomes column. (The homework and participation scores are quite lenient, so that students who are doing their homework and coming to class can easily meet the A-level for those requirements.)
The key idea here is that the outcomes the students have mastered are ones they really know. They have demonstrated that they can do these at a B+/A- level. The grades are determined by how many of the outcomes they have mastered.
Outcomes-Based Assessment Sends the Right Message
Let’s go back to the beginning and reconsider all those pedagogical ideals. What does our Outcomes-Based Assessment (OBA) structure tell students about them?
- Regular practice is important.
OBA: You have to be ready for our test every week.
- Carefully review exams and the solutions.
OBA: If you didn’t get it right this week, it will be on the test again next week, so you’d better review your work and our feedback. - It’s ok to get things wrong and learn from mistakes.
OBA: It doesn’t count against you when you get it wrong, but it does count *for* you when you get it right, even if it takes a while to get there. - The idea that we can improve through practice applies in math just as it would in anything else they want to learn.
OBA: You are rewarded just as much if you try a few times and then get it right as if you get it right on the first try. - “This test has not shown any gender or racial differences in performance or mathematical ability.”
I wish I could say with authority that OBA helps this. I don’t know yet. It seems like it should, since the whole point is that students can get feedback, learn what the expectations are, and then implement them. We’ll be setting up a multi-year study starting this year to learn more about the impacts (short and long term) of OBA on all of our Calculus students, but particularly on our students of underrepresented backgrounds. - We care primarily about your understanding of the math and communication of it.
OBA: This is precisely where we draw the line between when a student gets credit on a particular outcome and when they don’t. Students learn that the only way to succeed in our class is to review, revise, and to seek help when they don’t understand something. With OBA, students are much more likely than ever before to come in asking us to help them *understand* something, because they know that’s the only way they’re going to perform well enough to earn credit. - There’s no cap on the number of students who can get an A in this class.
OBA: This is just straight-up true. Any student who meets our threshold gets an A. End of story.
What’s the Catch?
For all my enthusiasm for this new system, I must admit there are some challenges.
The two biggest obstacles are:
- It takes a lot of work to set it up.
- There’s a lot of proctoring and grading time.
It took a fair amount of work to set up, especially for the first class we converted. (We started with Precalculus, which has a much smaller enrollment and fewer sections than our Calculus classes.) There are many decisions to make and details to iron out. You won’t get it perfect on the first try, so just go for it and adjust as you learn. We also spent a lot of time writing and proofreading problems for tests. Over time, we’re building a large problem bank, but the first semester really requires a lot of work on this.
Since there is a large start-up cost, it makes the most sense to convert classes that you teach regularly so you can reuse your work. But once you get the hang of it, it really seems like a better way to teach so it’s hard to go back to the traditional method.
We decided to test our students every week, and to have no restrictions on how many attempts they get at each outcome. This means that we’re proctoring and grading every week. It also means that if we have even one straggler who is struggling to get credit, we’re writing new problems for them every week. I know other people (including Jeff Ford) who do not test so often and/or restrict the number of times a particular outcome shows up on the tests. I think some restriction is better, both for the sanity of the faculty and because a little more pressure on the students means they have to follow up sooner and can’t just choose to put it off. We’re currently considering the pros and cons of different options for next fall.
Some other ongoing challenges include:
- Introducing the system to students
- Conveying students’ grades during the semester, particularly around drop decisions.
For most students, this structure is completely foreign. It’s absolutely necessary to spend some extra time introducing it and selling it to students. We hammer home the idea of “high frequency/low stakes” testing. I made a few videos to introduce the pedagogy to our students:
Some students are really anxious about it and have a hard time understanding at first. Most pick up on it after the first week or two, when they have seen all the components work in class.
It helps a LOT to have used the structure before. Our students who have experienced it typically love it, and are happy to endorse and explain it to students who are new to the system. We introduced Outcomes Based Assessment in our Single Variable Calculus sequence for the first time this fall (yes, along with moving online for Covid AND switching to a team-based learning format AND switching to a new textbook — can you say, “gluttons for punishment”?). Several students who took Differential Calculus this fall reached out to me to ask whether we would be using this system for Integral Calculus in the spring. They made it clear that they were only going to take Integral Calculus if we used Outcomes Based Assessment.
I still struggle with communicating to students what their grade is likely to be when we’re midway through the semester. In many ways, our grading is more transparent than the traditional system. Students know exactly where they stand at all times. They know what they already have learned and what they still need to work on. They can see clearly what they still need to do to get a particular letter grade. I built out individual spreadsheets for them to follow along with their progress. But, on the other hand, no one in the class is even passing until quite late in the semester. (I think this is right — after all, they haven’t even learned most of the material yet.) They have a hard time seeing if they’re on track to succeed, especially if they’re not getting everything right on the first try. And I have a hard time predicting what will happen. Will they get those outcomes they’ve been stuck on? Most will, but I can’t guarantee it.
Overall, our grades are higher. It seems that a lot of students who would probably have gotten B’s in the traditional system are able to get to A’s in this system. The system rewards good study habits and guides students on what they need to do so they can do it. And most students feel really comfortable in the last couple of weeks of classes, when they can see things slowing down and they don’t have much left to finish. But it’s hard in the middle to say which way things will break for students who are getting behind. I haven’t solved this problem yet.
This year probably would have been exhausting even without all this extra work we took on by introducing Outcomes Based Assessment. We’re definitely tired and ready to be done with proctoring and grading for the year. But even with all the challenges of online education, I think this structure has helped my students learn more and better than they did under our old, traditional structure.
Is it worth the hassle?
Yes.
Acknowledgements
If you got the idea in this article that I did all or most of this on my own, I apologize. It’s not true. This has been a multi-year team effort. Eric Hanson (mentioned above) was the one who wanted to try this out in the first place, and introduced us to Jeff Ford, who generously shared everything with us to help us get started.
My colleague, Keith Merrill, has been vital in making this work, along with many amazing graduate students (some former): Te Cao, Shujian Chen, Tarakaram Gollamudi, Abhishek Gupta, Simon Huynh, Shizhe Liang, Wei Lu, Ray Maresca, Ian Montague, Rose Morris-Wright, Rebecca Rohrlich, Alex Semendinger, Jill Stifano, and Jiajie Zheng.
Our initial implementation in our Precalculus course was supported by a Teaching Innovation Grant from the Provost’s Office and the Center for Teaching and Learning at Brandeis University.


Great and interesting article.
Thank you, my department is in the process of transitioning to a standards-based grading approach. This post will give us something to chew on.