Where to send a paper

Posted on December 25, 2021 by Edward Dunne

Suppose you have just written your first paper in an area and now you want to figure out where to send it.  Maybe it’s your first paper ever.  (If so, congratulations!)  Maybe you normally work in one area, but had a good idea in a neighboring subject that turned into a paper.  How can you determine some suitable journals for your paper?  A good idea is to ask colleagues.  Here is something you can do with MathSciNet, as a supplement to colleagues’ advice or in case no one has any good suggestions.

Continue reading →

Posted in Tips and Tricks | 1 Comment

Job posting – Associate Editor at Mathematical Reviews

Posted on December 2, 2021 by Edward Dunne

We are hiring!   We are looking for a new Associate Editor to start as soon as possible in 2022.   The job is posted on MathJobs.org (of course!).

Continue reading →

Posted in Jobs | Leave a comment

AMS Day 2021

Posted on November 29, 2021 by Edward Dunne

AMS Day banner

It’s AMS Day!

On Monday, November 29, 2021, 12:00 am- 11:59 pm Eastern Standard Time, we honor our AMS members via “AMS Day”, a day of specials on AMS publications, membership, and more. Our exciting limited-time offerings include:

  • Free access to MathSciNet®, the authoritative gateway to the scholarly literature of mathematics, for the day.
  • The first 133 purchases from the AMS Bookstore will receive a special gift: AMS branded socks for domestic purchasers or an AMS 2022 Math Imagery calendar for international purchasers!
  • Pay your 2022 dues today and lock in your AMS member benefits for up to 3 years at 25% off your dues rate for each additional year purchased. (3-year maximum and excludes Affiliate, Student, and Unemployed memberships).
  • Make a donation today and receive an AMS notebook.

Spread the word about #AMSDay today!

About our book discounts: Sale prices are valid for individual AMS members only, and may not be combined with any other discounts. Sale prices are valid for AMS published books only (no distributed titles are included in this offer).

Posted in Announcements | Leave a comment

MathSciNet for Developing Countries Program

Posted on November 20, 2021 by Edward Dunne

MDCMy latest column has been published in the Notices of the American Mathematical Society.  The topic is the MathSciNet for Developing Countries Program, or “MDC”, which was a topic in an earlier post about the program, with a focus on Uzbekistan.   That post was inspired by Scott Hershberger’s piece on the AMS web site.  Continue reading →

Posted in General information | Leave a comment

Are math papers getting longer?

Posted on October 14, 2021 by Edward Dunne

A page of nonsenseAt the September 2021 meeting of the AMS Committee on Publications, Nick Trefethen asked whether Mathematical Reviews has seen an increase in the average length of papers that come through for indexing in MathSciNet.  I had not thought about that question, and there isn’t an easy query for page length in the Math Reviews database.  During the overnight break, I looked into the data for Transactions of the American Mathematical Society. Afterwards, I looked at two more journals, Mathematics of Computation and Annals of Mathematics. Continue reading →

Posted in Data on publishing | 3 Comments

Lathisms $\cap$ Math Reviews = Andrés Caicedo!

Posted on September 29, 2021 by Edward Dunne

LathismsLathisms was founded in 2016 to showcase the contributions of Latinx and Hispanic mathematicians, especially during Hispanic Heritage Month, which is celebrated in the United States from September 15 and October 15 every year.  The featured mathematician for September 27, 2021, is Andrés Caicedo, an Associate Editor at Mathematical Reviews.  The link to their profile of Andrés is here. The profile is also available as a poster. Continue reading →

Posted in Mathematicians | Leave a comment

Winners of the 2022 Breakthrough Prizes in Mathematics

Posted on September 13, 2021 by Edward Dunne

Breakthrough Prize LogoThe winners of the 2022 Breakthrough Prizes have been announced.  There are eight recipients in mathematics:  Takuro Mochizuki, Aaron Brown, Sebastian Hurtado Salazar, Jack Thorne, Jacob Tsimerman, Sarah Peluse, Hong Wang, and Yilin Wang.

Continue reading →

Posted in Prizes and awards | Leave a comment

Computing Digits of $\pi$

Posted on August 20, 2021 by Edward Dunne

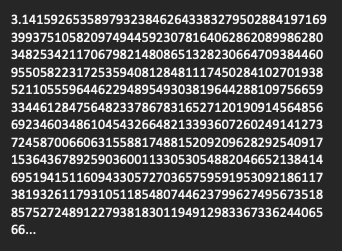A bit more than 500 digits of PiResearchers at the Fachhochschule Graubünden in Switzerland have announced the latest record for the number of digits of $\pi$ that have been computed. They have computed roughly 62.8 trillion digits using a supercomputer. Continue reading →

Posted in Mathematics in the news | Leave a comment

Yoshimura Crush Patterns

Posted on July 18, 2021 by Edward Dunne

Ceramic mugs in the shape of a Yoshimura crease patternOne of the signature moves of the John Belushi character in the movie Animal House is Belushi crushing an aluminum can against his forehead.  The shape of the crushed can presents an interesting problem in material science, which has a nice mathematical component. For perfectly symmetrically crushed cans, the shapes are known as Yoshimura Crush Patterns.  Continue reading →

Posted in Extra content, Math on the web | 3 Comments

Cicadas in MathSciNet

Posted on June 25, 2021 by Edward Dunne
Photo of a Brood X cicada

Photo: Michigan Department of Natural Resources

The cicadas of Brood X have emerged throughout much of the eastern United States.  In certain areas of Ann Arbor, Michigan, where Mathematical Reviews is  physically located, they have become quite loud.   They belong to the genus Magicicada of periodical cicadas that emerge either in 13-year cycles or in 17-year cycles.  The cycle lengths are prime numbers, which makes mathematicians wonder why.

Continue reading →

Posted in Mathematics in the news | Leave a comment