Suppose you have just written your first paper in an area and now you want to figure out where to send it. Maybe it’s your first paper ever. (If so, congratulations!) Maybe you normally work in one area, but had a good idea in a neighboring subject that turned into a paper. How can you determine some suitable journals for your paper? A good idea is to ask colleagues. Here is something you can do with MathSciNet, as a supplement to colleagues’ advice or in case no one has any good suggestions.
I’m going to discuss this by using the example of representations of p-adic Lie groups, a subject that is on the boundary of what I know.
Step 1. Figure out the MSC class that represents the subject area. If you managed to get some results and write a paper on the subject, you probably know a few papers in that area, or maybe some authors who work in the area. For p-adic Lie groups, I know that Paul Sally worked extensively in the area. Here are three papers by Sally that have “p-adic” in the title.
MR2798422
Adler, Jeffrey D. (1-AMER-MS); DeBacker, Stephen (1-MI); Sally, Paul J., Jr. (1-CHI); Spice, Loren (1-TXC)
Supercuspidal characters of SL2 over a p-adic field . (English summary) Harmonic analysis on reductive, p-adic groups, 19–69,
Contemp. Math., 543, Amer. Math. Soc., Providence, RI, 2011.
22E50
MR1039842
Sally, Paul J., Jr. (1-CHI)
Some remarks on discrete series characters for reductive $p$-adic groups. Representations of Lie groups, Kyoto, Hiroshima, 1986, 337–348,
Adv. Stud. Pure Math., 14, Academic Press, Boston, MA, 1988.
22E50 (22E35)
MR0744292
Moy, Allen (1-YALE); Sally, Paul J., Jr. (1-CHI)
Supercuspidal representations of SLn over a $p$-adic field: the tame case.
Duke Math. J. 51 (1984), no. 1, 149–161.
22E50
The class 22E50 is the primary classification for all three, with 22E35 as a secondary class on one of the papers. Looking up the descriptions of the classes, we find:
22E35 Analysis on p-adic Lie groups
22E50 Representations of Lie and linear algebraic groups over local fields [See also 20G05]
It helps to know a couple of things here. First, p-adic fields are local fields – indeed they are about the only examples of local fields I can think of without going to Wikipedia or MathWorld. Second, an important tool in studying representations of any sort of group is the analysis of the group’s characters, which are functions on the group related to the representations. So, I am confident that 22E50 and 22E35 are reasonable classes to use, with 22E50 likely to be better because “representations” occurs in the description.
Step 2. Do a Publications Search for MSC 22E50.
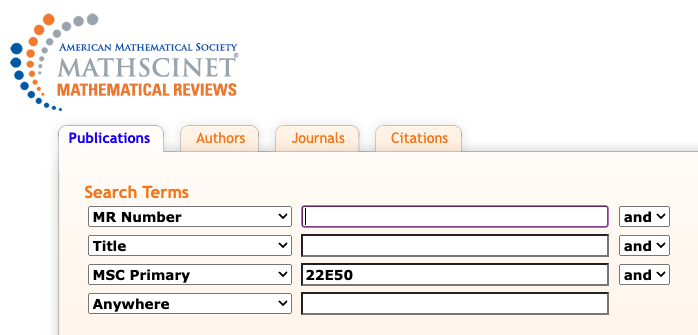
There are 1689 matches.
Step 3. In the search results, look in the sidebar under the heading “Journals”.
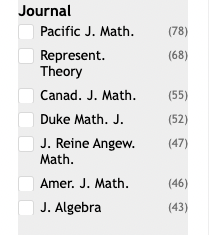
The journals are listed in decreasing order of the number of matches in the search results. Here are the journals that have at least 20 articles with MSC 22E50 as the primary class.
| Journal | Count |
| Pacific J. Math. | 78 |
| Represent. Theory | 68 |
| Canad. J. Math. | 55 |
| Duke Math. J. | 52 |
| J. Reine Angew. Math. | 48 |
| Amer. J. Math. | 46 |
| J. Algebra | 43 |
| Compositio Math. | 37 |
| J. Number Theory | 37 |
| Trans. Amer. Math. Soc. | 37 |
| Israel J. Math. | 36 |
| Manuscripta Math. | 36 |
| Invent. Math. | 33 |
| Math. Ann. | 33 |
| Ann. Sci. École Norm. Sup. (4) | 29 |
| Compos. Math. | 29 |
| Proc. Amer. Math. Soc. | 29 |
| Astérisque | 27 |
| Int. Math. Res. Not. IMRN | 27 |
| J. Lie Theory | 24 |
| J. Inst. Math. Jussieu | 23 |
| Bull. Soc. Math. France | 20 |
| C. R. Acad. Sci. Paris Sér. I Math. | 20 |
This gives you a list of journals to consider.
Step 4. These articles are all on representations of groups over local fields, which is going to be a fairly tight match due to the narrowness of the definition of the subject area. Some other classifications are broader, with more variations within the class. Consider, for instance, 94A08 Image processing (compression, reconstruction, etc.) in information and communication theory. This covers a lot of ground. Indeed, a search for MSC Primary = 94A08 produces 11986 matches. It might be sufficient to find a journal that publishes papers in image processing, but how close to the specific topic of your paper are they? Close enough? To look at the papers on image processing showing up in a particular journal, click on it in the sidebar. The search results are now filtered to include only papers from that journal. You can now look to see if they are close to the topic of your paper. If so, click on the journal’s name or abbreviation in any of the matches, which brings you to the MathSciNet profile page for that journal. You can then see information about the most frequently occurring authors in the journal, the most frequent 2-digit subject areas, the journal’s Math Citation Quotient (our computation of the number of citations divided by number of papers), and so on. There will also be a link to the journal’s website, where you will find information about how to submit a paper to the journal.
This method isn’t perfect, and isn’t a substitute for consulting experts, but it does give you a good list that is based on what the journal has published.
Some modifications.
Narrow the time-frame. Some journals have been around a long time. For instance, Pacific Journal of Mathematics started in 1951. It has published a lot of papers on representations of p-adic Lie groups, but what has it done recently? In Step 2, you could look for papers after the year 2000.
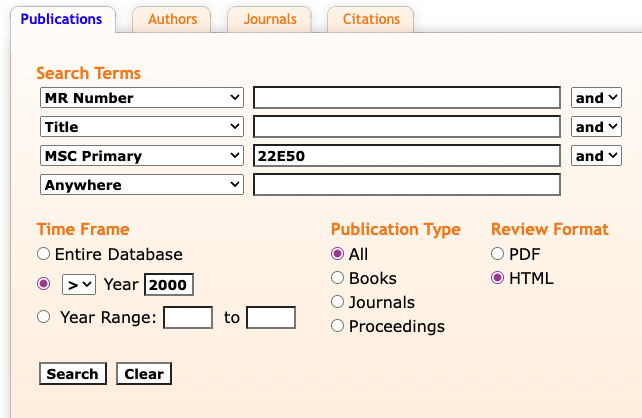
This produces 1026 matches. Here are the journals with the most articles meeting the criteria:
| Journal | Count |
| Represent. Theory | 63 |
| Pacific J. Math. | 42 |
| Canad. J. Math. | 40 |
| J. Number Theory | 34 |
| J. Algebra | 33 |
| Compos. Math. | 29 |
| Manuscripta Math. | 29 |
| Int. Math. Res. Not. IMRN | 27 |
| J. Reine Angew. Math. | 27 |
| Amer. J. Math. | 26 |
| Israel J. Math. | 23 |
| J. Inst. Math. Jussieu | 23 |
| Duke Math. J. | 22 |
| J. Lie Theory | 22 |
| Astérisque | 20 |
| Invent. Math. | 18 |
| Trans. Amer. Math. Soc. | 17 |
| Math. Z. | 16 |
| Proc. Amer. Math. Soc. | 16 |
| Bull. Soc. Math. France | 13 |
Search MSC Primary/Secondary. Some subject areas have fewer papers than others. For instance, if I had searched for MSC Primary = 22E35 and Publication Year > 2000, I would find only 132 matches. The journals with at least 3 papers matching the criteria are:
| Journal | Count |
| Int. Math. Res. Not. IMRN | 6 |
| Forum Math. | 5 |
| Pacific J. Math. | 5 |
| Trans. Amer. Math. Soc. | 5 |
| Canad. J. Math. | 4 |
| J. Funct. Anal. | 4 |
| C. R. Math. Acad. Sci. Paris | 3 |
| Canad. Math. Bull. | 3 |
| Israel J. Math. | 3 |
| J. Algebra | 3 |
| J. Inst. Math. Jussieu | 3 |
| Manuscripta Math. | 3 |
| Proc. Amer. Math. Soc. | 3 |
| Represent. Theory | 3 |
If I loosen the search to be MSC Primary / Secondary = 22E35 and Pub Year > 2000, the number of matches jumps to 403.
Combine classes. For the image processing example, where there were too many matches, you might search for both MSC Primary = 94A08 and something for an MSC Primary/Secondary class. For instance, wavelets are often used in image processing. You could add MSC 42C40 = Nontrigonometric harmonic analysis involving wavelets and other special systems to the search.
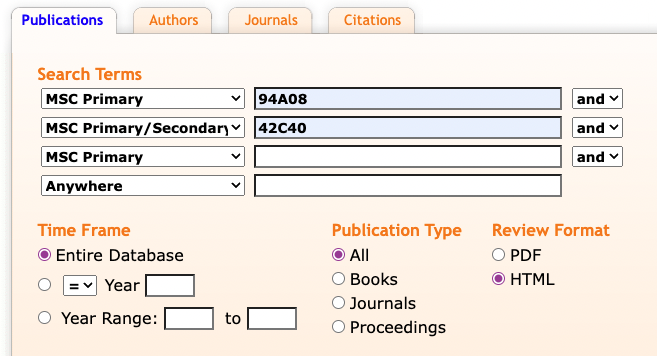
This was effective in that it cut the number of results down to just 217. The journals with at least five articles matching the criteria are:
| Journal | Count |
| IEEE Trans. Image Process. | 40 |
| Int. J. Wavelets Multiresolut. Inf. Process. | 29 |
| Appl. Comput. Harmon. Anal. | 16 |
| SIAM J. Imaging Sci. | 8 |
| J. Comput. Appl. Math. | 7 |
| J. Math. Imaging Vision | 5 |
I hope these suggestions are helpful. There is a lot of information in the Math Reviews Database that powers MathSciNet. It can be used in many different ways to help mathematicians, not all of which are pre-programmed into MathSciNet.

Dear Edward,
thank you for your help. I certainly will follow your hints to support our researchers.
Is there a chance to implement a filter that shows Golden OA-titles only?
Kind regards,
Antje