Getting Students Used to Abstract Concepts

According to my experience teaching limits in Calculus for Life Scientists, it is really difficult for students to understand limits because they do not have the required knowledge on which to build the concept. I have noticed that even if they can handle and apply the limit definition, problems often arise with their supposed prerequisite knowledge such as simplification, least common denominators, factoring, and long division. I had to make sure to spend the first two weeks of classes reviewing and refreshing what they had forgotten from their high school math classes.

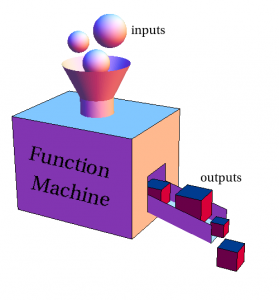
It can take a while for students to become comfortable with the idea and practice of treating functions as abstract objects. The function machine by Duane Q. Nykamp is licensed under a Creative Commons Attribution-Noncommercial-ShareAlike 4.0 License (http://creativecommons.org/licenses/by-nc-sa/4.0/).

However, after introducing limits, the students still encountered difficulties understanding the subtleties of one-sided versus two-sided limits. When you explain how to handle some types of functions, students will not pay attention to “some” because they only look at the outside definition without thinking about the internal meaning. In the beginning, it helped to give them instructions on how to approach very specific common types of functions such as roots, absolute value functions, piece-wise defined functions, and .

Another way I try to decrease the confusion for my students is to represent the function as a box and tell them that this box is a control system, which means that we have input and output.Therefore, if we have a number or variable as input, this number/variable needs to be plugged into any variable that appears in the box (I tell them that our function is inside the box). Then, after plugging in whatever we have as input, we will have the result which is the output. It also helps my students when I write math problems on the board in colors and sometimes with shapes because it is very helpful for students to focus on the functions and the changes we do to them.

Students are familiar with the usage of the variable in functions, say , but if we change that to , some students may not be able to plug in, say , to find . To avoid this confusion, I give them at least four examples: one with , one with , one with a Greek letter, and one with . This method can make students familiar with the usage of other variables in functions.

Similarly, when the students worked in groups for a class activity on functions, I noticed some other common mistakes. For example, suppose they are given and are asked to find . The first time I gave them a problem like that, they did not know where to plug in ; often they would plug it in as . I guided them to the step , but we ended up with another problem because they did not know how to simplify . They thought that . I always try to help students by writing handouts to address the common errors and how they can avoid making them on exams. (You can view the handout that I created on this topic here.)  When I see something is very difficult for them to understand using the traditional method, I create my own method using interactive techniques. (See my earlier blog post: How to change the Traditional Mathematics Teaching from the Memorization-Based Method to Interactive-Based Method.)

In conclusion, based on my experience, handling functions as abstract objects is one of the most difficult mathematical concepts for non-engineering and non-math students. I believe that a successful math teacher must teach students how to use advanced mathematical thinking in order to help them become more comfortable with abstract mathematical objects.

To see more teaching handouts, please see my course webpage. Best of luck and feel free to reach out if you have questions!