It’s Halloween time and kids will soon be trick-or-treating. But if your kids pool their candy, how can you make sure that each child receives a fair share? That’s where the method of markers can help!
The method of markers is a fair division method which is used when
- There are more items to be divided than there are players in the game.
- The items are reasonably close in value.
The method (for N players and M discrete items) can be described by the following process:
Preliminaries – The items are lined up in a random order. For convenience, the items are labeled 1 through M, going from left to right.
Step 1 (Bidding) – Each player independently divides the array of items into N segments by placing N-1 markers along the array. These segments are assumed to represent the fair shares of the array in the opinion of that player. In order to keep the method fair, the players must all place their markers at the same time. One way of achieving this is if all players submit sealed envelopes with the positions of their markers. Everyone is guaranteed to get a fair share because the segments for a particular player never overlap.
Step 2 (Allocations) – Scan the line of items from left to right until the first first marker is located. The player owning that marker (let’s call him or her P1) goes first and receives the first segment in his or her bid. (If there is a tie, it is broken randomly.) Since P1 has received his/her fair share, the rest of his/her markers are removed. We continue scanning the line of items from left to right, looking for the first second marker. The player owning that marker (let’s call him or her P2) goes second and gets the second segment in his or her bid (which corresponds to the segment between his/her first and second markers). Continue this process, assigning one segment of his/her bid to each player. The last player gets the last segment in his/her bid, which is to the right of his/her last marker.
Step 3 (Dividing Leftovers) – If there are items left over after every player has received a fair share, divide the leftovers among the players by some form of lottery. For example, the players could take turns choosing leftover items or, if there are many more leftover items than players, the method of markers could be used again.
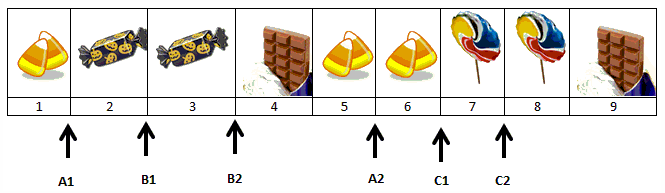
Consider the following example. Three children (Abby, Bryan, and Chloe) are dividing the array of nine candy pieces shown in the following figure using the method of markers. The players’ bids are indicated in the figure (with A for Abby, B for Bryan, and C for Chloe).
In this example, Abby would consider any one of these shares to be fair:
{1} (Abby’s 1st segment)
{2, 3, 4, 5} (2nd segment)
{6, 7, 8, 9} (3rd segment)
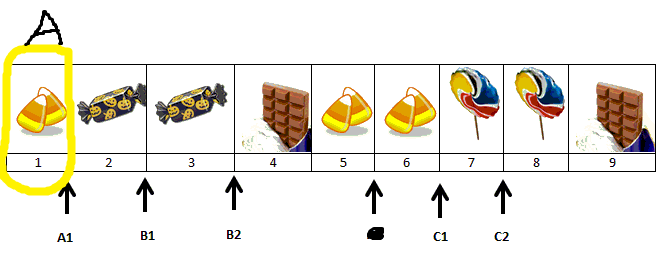
We start at the left-hand side of the line of candy and look for the first first marker (in this case, it is A1). Abby will go first and will receive the first segment in her bid:
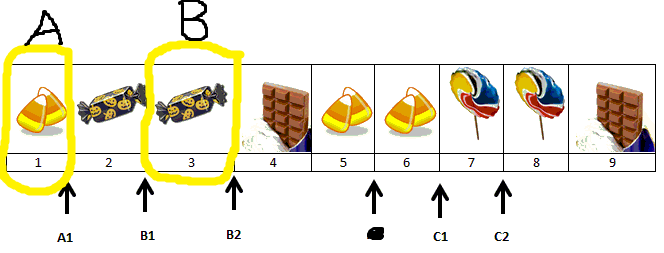
Notice that the rest of Abby’s markers have been removed since she has now received her fair share. We now continue scanning the line of items from left to right, looking for the first second marker. The next marker we come across is B1. However, since this is not a second marker we ignore it. The first second marker that we come across is B2. Bryan will go second and will receive the second segment in his bid:
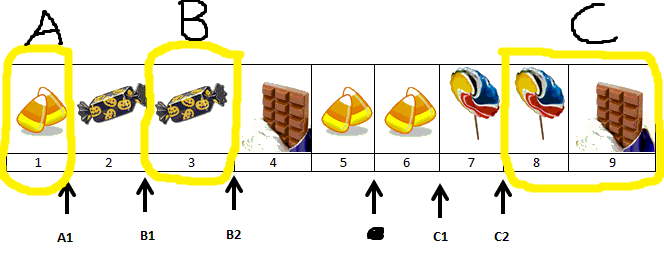
Now we are down to the last player, Chloe. Chloe will get the last segment in her bid, which is to the right of her last marker (i.e. to the right of her C2 marker):
In this example, the final allocation of candy is: Abby gets piece 1, Bryan gets piece 3, Chloe gets pieces 8 and 9, and pieces 2, 4, 5, 6, and 7 are all leftovers (which can be divided among the children using some form of lottery).
Despite its elegance, the method of markers can be used only under some fairly restrictive conditions. In particular, the method works best if the items are roughly equivalent in value to each other and if the players’ preferences are fairly close. This is almost impossible to accomplish when there is a combination of expensive and inexpensive items, but is perfect for dividing items that are of small and equal value (like candy). So go out and enjoy, knowing you are now equipped with a method to fairly split the spoils from trick-or-treating. Happy Halloween!
Sources:
Tannenbaum, Peter. Excursions in Modern Mathematics (Sixth Edition). Upper Saddle River, N.J: Pearson Prentice Hall, 2007.