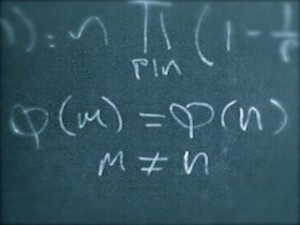Carmichael’s Totient Conjecture

Photo Credit: Avery Carr

In the wake of mathematical enlightenment a profound understanding of basic notions bridges the gap between the conceptual and concrete.   In many cases, problems that have an exterior of simplicity exploit the boundaries of comprehension and provide insight into extensive associations.  From the mind-stretching inclinations of geometry and algebra emerges the intricate framework from which these connections form.  Piece by piece, generalizations are built from the material of empirical understanding fabricated by the process of asking intrinsic questions.

Questions of this nature are entwined in reticent patterns found across the full spectrum of mathematics.   Many of these inquiries encompass and ascertain the properties of special functions.     Mappings such as Euler’s Totient function provide a strong basis for further investigation into characteristics of positive integers.   Specifically,  this function denoted by   counts the number of positive integers less than or equal to a positive integer such that the positive integers counted and have only 1 as their common divisor (in other words they are relatively prime to , denoted  such that  ).   In example,  =    because there are two positive integers less than or equal to 3 that are relatively prime to 3 (namely 1 and 2, given ). Euler’s Totient function is distinguished by several other properties as well.    For instance, if is a prime number, then .   It is also multiplicative, in the sense that if  then   = .   By virtue of these attributes, several open problems in the field of number theory involve .

The mathematician Robert Carmichael proposed one such conundrum in 1907 that still remains unsolved.   Basically,  Carmichael conjectured that for every positive integer there exists a positive integer such that   and .   As a consequence, with the given properties, the conjecture is certainly true for odd numbers.  This can be seen by letting be a positive odd integer and in the fact that  =  , which it follows               

= = .

However,  as easily proved as the conjecture is for the positive odd integers,  the statement has not been shown true for the positive even integers.   Maybe a clever argument will come from a thorough investigation of basic notions.    Perhaps, rather, it will be stumbled upon in search of greater abstractions.  Whatever the case of discovery may be, a resolution will certainly be achieved, if at all, by asking insightful questions.