A guest post from Reginald Anderson at Kansas State University.
First-time learners of calculus often struggle with the notion of an infinitesimal, and considering $\frac{dy}{dx}$ literally as a fraction can lead students astray in Calculus III and differential equations, when implicit differentiation and separable equations rely on the chain rule in ways that strongly contradict any consideration of $\frac{dy}{dx}$ as a literal fraction. However, literality can be restored by considering infinitesimals algebraically as nilpotents, which is exactly the claim that one is free to ignore all but a finite number of terms of a Taylor series for a smooth analytic function. Algebraic geometry offers methods of ‘zooming in on a point’ to consider local phenomena in ways that reveal an algebraic structure to infinitesimals which can console newcomers to calculus (“just look at the linear part!”) and restore the desire to take infinitesimals literally. Here, I offer one framework for viewing infinitesimals as dual numbers which is not new, though the connection I make to complex algebraic geometry shows that what one learns in advanced graduate coursework is in keeping with a traditional undergraduate curriculum.
For $f$ a smooth, analytic function defined on the real line, the linear part of its Taylor Series approximation is given by the differential. Scheme-theoretically, one can view infinitesimal neighborhoods of a point of $\mathbb{R}$ as isomorphic to the dual numbers, or an algebraic generalization thereof. For $\mathbb{D}:= \mathbb{R}[\epsilon] = \mathbb{R}[x]/(x^2)$, one representation of the dual numbers comes from \[ \mathbb{D} \cong \{a+b\epsilon\text{ }|\text{ }a,b\in \mathbb{R} \text{ and }\epsilon^2=0 \} \cong \left\{ \left[\begin{matrix} a & b \\ 0 & a \end{matrix}\right] \text{ }|\text{ }a,b\in \mathbb{R} \right\}. \]
For $Z\subset X$ an irreducible subscheme, the $\mu$-th infinitesimal neighborhood of $Z$ is denoted and constructed by \[ Z_\mu := \{ Z, ^{\mathcal{O}_X}/_{\mathcal{I}^{\mu + 1}} \}. \]
The same construction can be carried out for $\{a\} \subset \mathbb{R}$ considered as an irreducible subvariety, even though $\mathbb{R}$ is not algebraically closed, where $\{a\}$ is given by the ideal sheaf \[ \mathcal{I} = \begin{cases} (x-a) & \text{ over any open set containing }a\\ (0) & \text{ otherwise. }\end{cases}\] This implies that the first infinitesimal neighborhood of the point $Z=\{a\}$ is \begin{align*} Z_1 := \{ Z, ^{\mathcal{O}_\mathbb{R}}/_{\mathcal{I}_Z^2} \},\end{align*}
and for $U$ any open set of the real line containing the point $a$, $\mathcal{I}$ assigns the ideal $(x-a)\subseteq \mathcal{R}[x]$ to $U$ so that over $U$,
\begin{align*}
Z_1:= \{ \{a\}, ^{\mathbb{R}[x]}/_{(x-a)^2} \} \end{align*}
and substituting $a=0$ gives
\begin{align*}
Z_1 :&= \{ \{0\}, ^{\mathbb{R}[x]}/_{(x-0)^2} \} \\
&= \{ \{ 0 \}, ^{\mathbb{R}[x]}/_{(x^2)} \}. \end{align*}
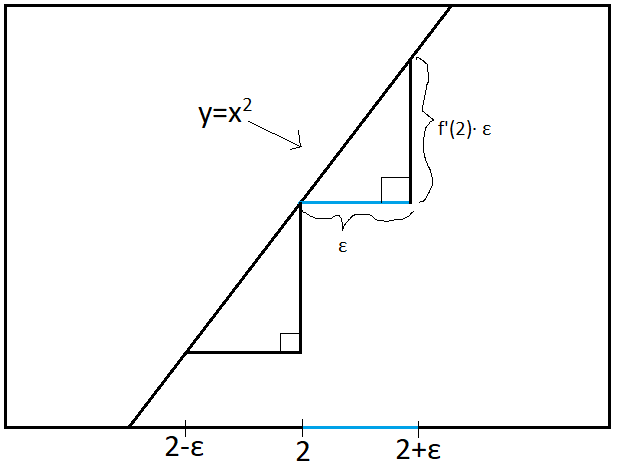
Now, the ring associated to the the point $0$ is $\mathbb{R}[x]/(x^2) \cong \{a+b\epsilon \text{ }|\text{ }a, b\in \mathbb{R}\text{ and } \epsilon^2=0 \} \cong \mathbb{D}$, which is the desired isomorphism mentioned above. To illustrate the connection with infinitesimals, Figure 1 shows the graph of $y=x^2$ in the real 2-dimensional plane, and Figure 2 shows the graph of $y=x^2$ “in the limit” at the point $(2,4)$. This concept can at times be hard for undergraduate students and new learners of calculus to grasp, though the fact that an algebraic structure is present in infinitesimals can be reassuring, once one understands that we have simply varied the square of the imaginary unit from -1 to solve $x^2+1=0$ over the real numbers, to simultaneously solving $x^2=0$ and $x\neq 0$.
Figure 1: Graph of $y=x^2$
Figure 2: Graph of $y=x^2$ in the Limit
The derivative of a function of a dual variable can be defined to agree with the real case: What is an Infinitesimal?. This has applications to, and can be interpreted with Lie algebras and tangent bundles. Matrix representations exist for higher order infinitesimal neighborhoods of a point of the real line, which encode higher order derivatives of a function matrically. Graduate students should have a good understanding of infinitesimals both in terms of Taylor Series approximations to smooth analytic functions, and of nilpotent elements in the ring of coordinate functions of a variety and their relation to each other in order to impart these concepts clearly to undergraduate students.
Further Reading
1. Fulton, William, and Joseph Harris. Representation Theory: a First Course. Springer, 2004.
2. Griffiths, Phillip, and Joseph Harris. Principles of Algebraic Geometry. Wiley, 1978.
3. Humphreys, James E. Linear Algebraic Groups. Springer, 2004.
4. Mora-Camino, Felix, and Carlos Alberto Nunes Cosenza. Fuzzy Dual Numbers: Theory and Applications. Springer, 2018.
5. Tu, Loring W. An Introduction to Manifolds. Springer, 2011.
