RSA Encryption – Keeping the Internet Secure |

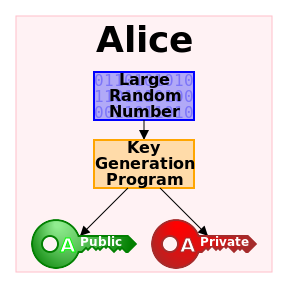
A flowchart describing the process of generating a public and private key. Photo acquired from Wikimedia Commons, the free media repository

We use the Internet for many things, from reading news articles, to keeping in touch with friends on social media, to shopping from the comfort of our own homes. Many of these tasks involve sending sensitive personal information (such as credit card numbers and our home address) to complete strangers. We would like to keep this information safe, making sure no malicious third party is able to intercept our messages. RSA is a cryptosystem which is known as one of the first practicable public-key cryptosystems and is widely used for secure data transmission. RSA has stood the test of nearly 40 years of attacks, making it the algorithm of choice for encrypting Internet credit-card transactions, securing e-mail, and authenticating phone calls.

One of the distinguishing techniques employed in public-key cryptography is the use of asymmetric keys. In this scheme, one key (the public key) is used to encrypt the message while a different key (the private key) is used to decrypt it. The keys are related mathematically, but the parameters are chosen so that calculating the private key from the public key is either impossible or prohibitively expensive.

At MIT in the fall of 1976, computer scientists Ronald Rivest and Adi Shamir, along with number theorist Leonard Adleman devised the public-key encryption code that bears their initials (RSA encryption), and has been in use ever since to secure electronic transactions. The RSA algorithm was the culmination of many months of work, which all started when Rivest read a paper by Diffie and Hellman, proposing that a good public-key encryption scheme would need to be based on what they called a “trap-door one-way function.” This function would be easy to compute, but hard to invert unless you knew the secret (the “trap door”). Rivest and Shamir would come up with numerous number theoretic schemes to fit this “trap door” idea, and then Adleman would try to poke holes in it (usually succeeding after a few minutes’ thought). However, one evening Rivest called Adleman with a new idea, which Adleman agreed was a good one because it seemed that only factoring would break the algorithm. Rivest wrote up a paper about the new algorithm and sent a copy to Adleman. The authors were listed in the standard alphabetic order: Adleman, Rivest, and Shamir. Adleman objected to this ordering, however, because he stated that he had not done enough work to be listed first. Adleman consented to being listed as an author only if his name was put last, reflecting what he considered his minimal contribution. Adleman said later, “I remember thinking that this is probably the least interesting paper I will ever write and no one will read it and it will appear in some obscure journal.” The paper in question was published in Communications of the ACM and so the RSA (instead of the ARS) algorithm was born.

The RSA algorithm involves three steps: key generation, encryption, and decryption. RSA involves two keys – a public key and a private key. As the names suggest, anyone can be given information about the public key, whereas the private key must be kept secret. Anyone can use the public key to encrypt a message, but only someone with knowledge of the private key can hope to decrypt the message in a reasonable amount of time. So how are these keys generated? The power and security of the RSA cryptosystem is based on the fact that the factoring problem is “hard.” That is, it is believed that the full decryption of an RSA ciphertext is infeasible because no efficient algorithm currently exists for factoring large numbers. The keys for the RSA algorithm are generated as follows:

1. Choose two distinct prime numbers $p$ and $q$ . In order for the system to be secure, the integers $p$ and $q$ should be chosen at random and should be of similar bit-length. To find large primes, the numbers can be chosen at random and, using one of several fast probabilistic methods, we can test their primality.

2. Compute $n = pq$ . The product $n$ will be used as the modulus for both the public and private keys. Its length, usually expressed in bits, is the length of the key.

3. Compute $\varphi (n) = \varphi (p)\varphi (q) = (p-1)(q-1)$ , where $\varphi$ is Euler’s totient function.

4. Choose an integer $e$ such that $1 < e < \varphi (n)$ and gcd $(e, \varphi (n)) = 1$ (that is, $e$ and $\varphi (n)$ are coprime). The number $e$ is released as the public key exponent.

5. Determine $d$ as $d \equiv e^{-1}$ mod $\varphi (n)$ . That is, $d$ is the multiplicative inverse of $e$ (modulo $\varphi (n)$ ). This is often computed using the extended Euclidean algorithm. The number $d$ is kept as the private key exponent.

The public key is formed by the pair $(n, e)$ , where $n$ is called the modulus and $e$ is called the public (or encryption) exponent. The private key is formed by the pair $(n, d)$ , where $d$ is called the private (or decryption) exponent. It is imperative that the decryption exponent $d$ is kept secret. In addition, the numbers $p, q$ , and $\varphi (n)$ must also be kept private because they can be used to calculate $d$ .

Once the keys are determined, secure messages can now be sent. Suppose Bob would like to send Alice a message. Alice transmits her public key $(n, e)$ to Bob, keeping her private key secret. In order to send Alice an encrypted message, Bob first has to turn the message $M$ into an integer $m$ , such that $0 \leq m < n$ . This is done by using a previously agreed-upon reversible protocol known as a padding scheme. Bob then computes the ciphertext $c$ corresponding to his message. The ciphertext can be found by computing $c \equiv m^{e}$ (mod $n$ ). Bob then transmits the encoded message $c$ to Alice. In order to recover the message, Alice uses her private key, computing $m \equiv c^{d}$ (mod $n$ ). Given $m$ , she can recover the original message $M$ by reversing the padding scheme.

We will now look at a small (and insecure) example. Alice would like to create a public and private key to use for her secure internet transactions. In order to create these keys, she chooses $p = 101$ and $q = 113$ . Next, she computes $n = pq = 11413$ as well as the totient $\varphi (n) = (p-1)(q-1) = 11200$ . In order to find the public key exponent, Alice must choose a number $1 < e < 11200$ which is also coprime to 11200. For this example, Alice will choose $e$ = 3533. Finally, Alice must compute $d \equiv e^{-1}$ (mod $\varphi (n)$ ) = 6597. Alice publishes the public key pair $(n = 11413, e = 3533)$ , while keeping $p, q,$ and $d$ private. Now suppose that Bob would like to send the message $m = 9726$ to Alice. Bob would compute

$c \equiv 9726^{3533}$ (mod $11413$ ) = 5761,

which he would then send to Alice. After receiving the ciphertext $c$ , Alice can decode the message using her private key

$m \equiv 5761^{6597}$ (mod $11413$ ) = 9726.

The RSA algorithm has remained a secure scheme for sending encrypted messages for almost 40 years, earning Rivest, Shamir, and Adleman the Association for Computing Machinery’s 2002 Alan Turing Award, among one of the highest honors in computer science. Currently, the only way to completely break the RSA cryptosystem in use today (which is slightly more sophisticated than that described here) is to factor the modulus $n$ . With the ability to recover the prime factors $p$ and $q$ , an attacker can compute the secret exponent $d$ from the public key $(n,e)$ . Once they have the secret exponent, the attacker can decrypt any message sent using the public key. What keeps RSA safe from such an attack is the fact that no polynomial-time algorithm for factoring large integers on a classical computer has been found yet. However, it also has not been proven that no such algorithm exists. As of 2010, the largest known number factored by a general-purpose factoring algorithm was 768 bits long, using a state-of-the-art distributed implementation. RSA keys are typically 1024 to 2048 bits long, though some experts believe that 1024-bit keys could be broken in the near future. It is generally believed that 4096-bit keys are unlikely to be broken in the foreseeable future, meaning that RSA should remain secure as long as $n$ is chosen to be sufficiently large. It is currently recommended that $n$ be at least 2048 bits long.

In 1994, Peter Shor showed that a quantum computer could be used to factor a number $n$ in polynomial time, thus effectively breaking RSA. Stay tuned for my next article where we will look at Shor’s algorithm in depth!

Sources:

Robinson, Sara. “Still Guarding Secrets after Years of Attacks, RSA Earns Accolades for its Founders.” SIAM News, Volume 36, Number 5, June 2003.

R. L. Rivest, A. Shamir, and L. Adleman. 1978. A method for obtaining digital signatures and public-key cryptosystems. Commun. ACM 21, 2 (February 1978), 120-126. DOI=10.1145/359340.359342 http://doi.acm.org/10.1145/359340.359342

RSA Encryption – Keeping the Internet Secure

About Stephanie Blanda

2 Responses to RSA Encryption – Keeping the Internet Secure

Categories

Archives

Retired Blogs

Meta