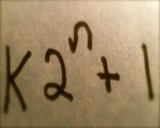The legendary math Universalist, Henri Poincare, once said, “ Mathematicians do not study objects, but relations between objects.” Inspired by subtle patterns that emanate from an abyss of ostensible chaos, mathematicians manifest these words by exploring relations within algebraic and geometric structures. These edifices, upon occasion, reveal intricate beauty buried deep in a profusion of symbols etched on the tablet of logical thought. Problems requiring various degrees of acumen have been presented in an assortment of publications over the course of modern history. From the field of Number Theory, problems are often innocently conveyed, but cloaked behind a veil of extensive logic that guards them from any immediate proof. Some problems call for a deep understanding harnessed only after years of study. However, others are immediately accessible with a little mathematical maturity. One such conundrum can be stated in terms of Sierpiński numbers of the second kind. A Sierpiński number of the second kind (henceforth, just Sierpiński number) is an odd positive integer such that
is a composite number for every positive integer
. In 1960, Wacław Sierpiński proved that there are infinitely many such
. To eliminate a given positive integer
from Sierpiński number candidacy, one only needs to show a prime number of the form
for some positive integer
. On the other hand, to prove that
is a Sierpiński number, the convention is to show that there exists a covering set of primes such that every member of the set divides
for every positive integer
. The smallest Sierpiński number currently known is 78557 and was proven by the mathematician John Selfridge in 1962 with the covering set { 3, 5, 7, 13, 19, 37, 73 }. Therefore, a fundamental open question arises: Out of the set of all Sierpiński numbers, is 78557 the smallest? To answer this question in the affirmative, one has to eliminate all positive integers less than 78557 from Sierpiński number candidacy. Mathematical proof and computational methods have eliminated all but six remaining candidates: 10223, 21181, 22699, 24737, 55459, and 67607. The website Seventeen or Bust is a distributed computing project dedicated to the goal of eliminating these remaining six. When the project first started there were seventeen (hence the name), but since then, eleven have been eliminated by finding the desired prime. Anyone can join the search. It could be you that proves that 78557 is the smallest Sierpiński number. All one needs is a computer and a willingness to give up a small amount of computational power. So plug in and discover.
-
Opinions expressed on these pages were the views of the writers and did not necessarily reflect the views and opinions of the American Mathematical Society.
Categories
- Academic Skills
- Advice
- Algebra
- Algebraic Geometry
- AMS
- Analysis
- Announcement
- Arts & Math
- Biology
- Book Reviews
- Conferences
- Crossword Puzzles
- Diversity
- Ecology
- Editorial Statement
- First-generation
- General
- Grad School
- Grad student advice
- Grad student life
- Interview
- Interviews
- JMM
- Jobs
- Linear Algebra
- MAM
- Math
- Math Education
- Math Games
- Math History
- Math in Pop Culture
- Math Teaching
- Mathematicians
- Mathematics in Society
- Mathematics Online
- News
- Number Theory
- Publishing
- puzzles
- Social Justice
- Starting Grad Schol
- Statistics
- staying organized
- Teaching
- Technology & Math
- Topology
- Uncategorized
- Voting Theory
Archives
- December 2021
- November 2021
- October 2021
- September 2021
- April 2021
- January 2021
- November 2020
- July 2020
- June 2020
- May 2020
- March 2020
- February 2020
- January 2020
- December 2019
- November 2019
- October 2019
- September 2019
- August 2019
- November 2018
- September 2018
- June 2018
- May 2018
- March 2018
- February 2018
- January 2018
- December 2017
- November 2017
- October 2017
- September 2017
- August 2017
- July 2017
- June 2017
- April 2017
- March 2017
- February 2017
- January 2017
- December 2016
- November 2016
- October 2016
- September 2016
- August 2016
- July 2016
- June 2016
- May 2016
- April 2016
- March 2016
- February 2016
- January 2016
- December 2015
- November 2015
- October 2015
- September 2015
- July 2015
- June 2015
- May 2015
- April 2015
- March 2015
- January 2015
- December 2014
- November 2014
- October 2014
- September 2014
- August 2014
- July 2014
- June 2014
- May 2014
- April 2014
- March 2014
- February 2014
- January 2014
- December 2013
- November 2013
- October 2013
- September 2013
- August 2013
- July 2013
- June 2013
- May 2013
- April 2013
- March 2013
- February 2013
- January 2013
- December 2012
- November 2012
- October 2012
- September 2012
- August 2012
- July 2012
- June 2012
- May 2012
- April 2012
- March 2012
- February 2012
- January 2012
- December 2011
- November 2011
- October 2011
- September 2011
- August 2011
- July 2011
- June 2011
- May 2011
- April 2011
- March 2011
- February 2011
- January 2011
- December 2010
- November 2010
- October 2010
- September 2010
- August 2010
- July 2010
- June 2010
- May 2010
- April 2010
- March 2010
- February 2010
- January 2010
- December 2009
- November 2009
- October 2009
- September 2009
- August 2009
- July 2009
- June 2009
- May 2009
- April 2009
- March 2009
- February 2009
Meta