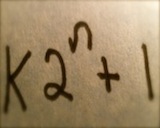Sierpiński Or Bust

Photo Credit: Avery Carr

The legendary math Universalist, Henri Poincare, once said, “ Mathematicians do not study objects, but relations between objects.”  Inspired by subtle patterns that emanate from an abyss of ostensible chaos, mathematicians manifest these words by exploring relations within algebraic and geometric structures.  These edifices, upon occasion, reveal intricate beauty buried deep in a profusion of symbols etched on the tablet of logical thought. Problems requiring various degrees of acumen have been presented in an assortment of publications over the course of modern history.   From the field of Number Theory, problems are often innocently conveyed, but cloaked behind a veil of extensive logic that guards them from any immediate proof.   Some problems call for a deep understanding harnessed only after years of study.   However, others are immediately accessible with a little mathematical maturity.   One such conundrum can be stated in terms of Sierpiński numbers of the second kind.   A Sierpiński number of the second kind (henceforth, just Sierpiński number) is an odd positive integer such that is a composite number for every positive integer . In 1960, Wacław Sierpiński proved that there are infinitely many such .    To eliminate a given positive integer from Sierpiński number candidacy, one only needs to show a prime number of the form for some positive integer .  On the other hand, to prove that is a Sierpiński number, the convention is to show that there exists a covering set of primes such that every member of the set divides for every positive integer . The smallest Sierpiński number currently known is 78557 and was proven by the mathematician John Selfridge in 1962 with the covering set { 3, 5, 7, 13, 19, 37, 73 }. Therefore, a fundamental open question arises:  Out of the set of all Sierpiński numbers, is 78557 the smallest?  To answer this question in the affirmative, one has to eliminate all positive integers less than 78557 from Sierpiński number candidacy.  Mathematical proof and computational methods have eliminated all but six remaining candidates: 10223, 21181, 22699, 24737, 55459, and 67607. The website Seventeen or Bust is a distributed computing project dedicated to the goal of eliminating these remaining six.    When the project first started there were seventeen  (hence the name),  but since then,  eleven have been eliminated by finding the desired prime.  Anyone can join the search.     It could be you that proves that 78557 is the smallest Sierpiński number.   All one needs is a computer and a willingness to give up a small amount of computational power.  So plug in and discover.