Infinity Elephants and Gabriel’s Horn

Guest Author: Brian Hook

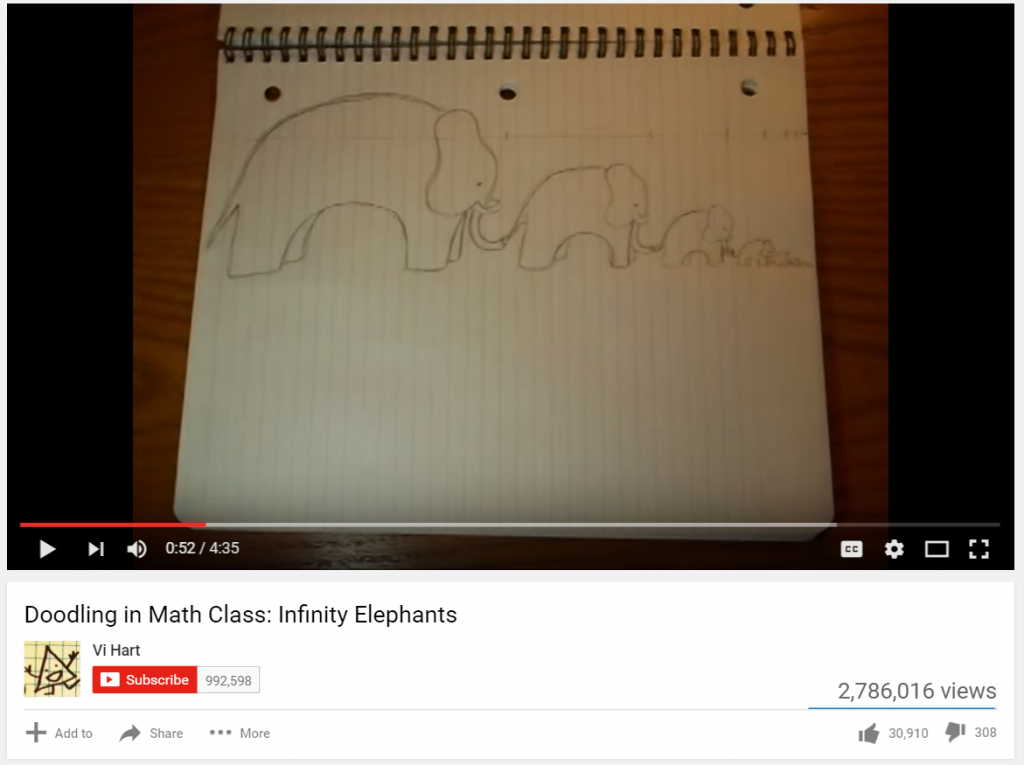
A screenshot of Vi Hart’s “Infinity Elephants” video which creatively addresses infinite series.

Vi Hart’s Doodling in Math Class: Infinity Elephants is a fun little video that brushes over many mathematical concepts without getting bogged down in technical jargon. Vi, a prolific recreational mathematician who also contributes heavily to Khan Academy, starts the video off by discussing infinite series such as ½ + ¼ + 1/8 + 1/16 + 1/32 + … = 1 and the issue of convergence of series. As you can see in the screenshot here, Vi draws elephants of length  ½, 1/4, 1/8… of a page and relates this drawing to the idea of convergent series.

Watching the video reminded me of the dilemma with Gabriel’s Horn, a famous example of a shape that is infinite in length and surface area but finite in volume. Gabriel’s Horn is a useful example to employ in calculus classes to help students visualize integration in three dimensions while showing that some infinite shapes have finite volume.

3D rendering of Gabriel’s horn from the public domain.

This is often seen as an object that can be filled with paint but not painted, and it was pointed out that since the shape is unbounded it would take infinite time to fill it. This is where we connect to Vi’s problem: bounding an infinite shape in a finite space.

The way Mark Lynch decided to tackle this problem is by making it into a piecewise function: on is defined as if or if is a positive integer and on the interval . This makes a spiked looking shape that has the same principles as Gabriel’s Horn but is bounded. When bounding Gabriel’s Horn and shifting the focus to a piecewise function, our problem becomes a geometric series and we can explicitly compute the area.

The way Vi found her answer was a bit different; she looked to fractals for her approach. Problems like these have many applications and have many ways of solving them from integration to piecewise functions to fractals. However you look at these types of problems, the good news is that you will always have many further questions to pursue.

Sources:

• Fleron, Julian F. “Gabriel’s Wedding Cake.” The College Mathematics Journal 30.1 (n.d.): 35-38. Web.
• Hart, Vi. “Doodling in Math Class: Infinity Elephants.” YouTube. YouTube, 02 Dec. 2010. Web. 08 Apr. 2016.
• “How-To Help and Videos – For Dummies.” How-To Help and Videos – For Dummies. N.p., n.d. Web. 08 Apr. 2016.
  Lynch, Mark. “A Paradoxical Paint Pail.” The College Mathematics Journal 36.5 (n.d.): 402-04. Web.
• http://www.matharticles.com/ma/ma044.pdf
• http://www.skepticink.com/reasonablyfaithless/2013/10/02/painting-gabriels-horn/