
Almost anyone in the math world will know that today is π Day. Every year on March 14, the date reads 3/14, the first 3 digits of our favorite constant. It may be an irrational holiday, but it is about the best that mathematicians get, and it seems to get more popular each year. Some of my Calculus II students discovered my favorite new way to write π on their final exam today. I found this by chance as I was trying to come up with a suitably difficult problem for them to solve. Here it is:
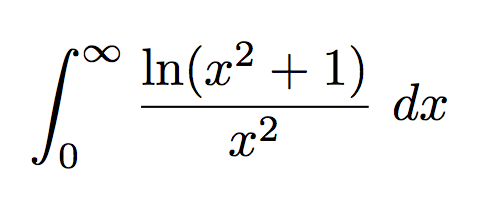
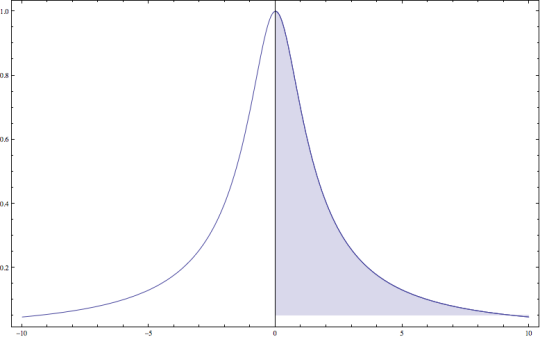
The function inside this integral has a wonderful graph shown below, and the integral above represents the area under the graph on the right side, stretching all the way to infinity– an extremely long and thin slice of π. (If you want to solve this integral without any hints, read no further!)
As Calculus II problems go, this one is a monster. First, it is improper at both limits of the integral (it is undefined at 0, and ∞ is always improper), so technically you should to split it into two integrals and take a limit of the bounds at either end. To make things worse, you have to integrate by parts, which may not be obvious at first. I’ll let you work it out on your own, but you will end up with exactly π, thanks to an arctangent function showing up along the way. I doubt I’m the first to find this integral, but I don’t yet see it on Wolfram’s list of integral representations of π (feel free to send me a check when you update this, Wolfram).
While you are working on this integral, I hope you are enjoying some pie as well (which you might find being sold for $3.14 today).
Happy π Day!
