A new school year is upon us, bringing new classes to teach or to take, depending on your year, new classmates to mentor or intimidate, depending on your mood, and in the illustrious high-paying danger-and-intrigue-filled world of grad student math blogs, a new editor-in-chief. Our outgoing editor-in-chief Tyler Clark of crossword-puzzle-making fame left big shoes to fill, and thus I hope that those of you who have been active on the blog in the past, as well as those discovering it for the first time, will join me in making it a success. If you are currently a masters student, PhD student, postdoc, person with valuable advice to share with the aforementioned shady characters, or just a lost soul in math or some math-esque discipline, come write for us! You could even earn yourself a coveted spot on our world famous “AMS Grad Student Blog Editorial Board,” guaranteed to earn you fortune and fame. Please contact me using the form below this post.
To kick off the new year (school year, Congressional fiscal year, Jewish/Gujarati/French Revolutionary calendar year, etc.), I’ll present a new type of puzzle. And by new, I mean new to most of you, I hope:
If you flew Southwest Airlines in that nameless decade that preceded this one, before they morphed into a more-or-less-generic mainstream megacarrier, perhaps you miss their reputation for funny flight attendants who made jokes about the safety instructions as you fastened your seatbelt low and tight across your waist. Or perhaps you long for their stunningly philo-procrastinatic-policy of allowing one to cancel one’s flight, sans penalty, up to two hours AFTER the flight took off. Yet when I look back on my dozens of disturbingly low-cost flights between BWI and Albany as I shuttled between my parents’ home in Washington, DC and my undergraduate studies at Williams College, I dream about Spirit, their old in-flight magazine. At the back of each issue wedged between the bland articles and complex flight maps, the latter of which may have led me to study graph theory, was a puzzle I have never seen before or since…until now. Shinro, a Japanese minesweeper-Sudoku hybrid, entertained me for countless hours…well, probably a dozen hours all told since there were only four puzzles per month and each took only 10-20 minutes. I found it more relaxing and less frustrating than Sudoku, especially for those like me who prefer making big fat X’s and circles rather than trying to juggle dozens of tiny digits. Here’s how it works:
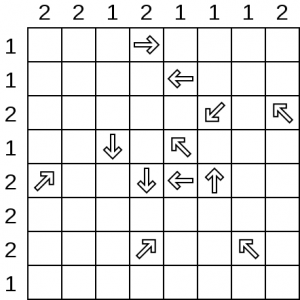
Each arrow in the puzzle below points to one or more “holes”. The numbers on the side indicate the number of holes in a given column or row. [Both images in this post are public domain, courtesy of Wikimedia Commons]
If you look in the first row, you’ll note that there can be only one hole and furthermore there is an arrow pointing to it. Therefore, the first three boxes prior to the arrow can be crossed off (rather like clicking on a “safe” tile in minesweeper). Similarly, the last three boxes in row two can be eliminated. Once you’ve done that, it becomes clear that the diagonal arrow at the end of row three must be pointing to a hole in the top row since you’ve crossed out the only other option. Once that hole is marked, the rest of the boxes in the top row can be eliminated, and so forth. The solution is below: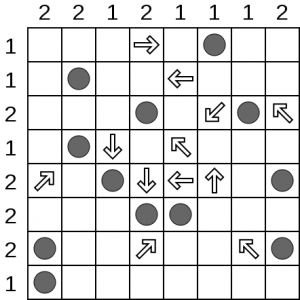
You can download Shinro to your Android or your iPhone here, though it goes by a couple other names. For those like me who enjoy the satisfaction of marking up a puzzle with a pencil (or for the overly-confident, a pen), David Oranchak offers a free book of Shinro which you print out for free here or order from Amazon for $12.95. If you run out, never fear, Oranchak claims there are over 1,000,000,000,0…[25 more zeros]…00,000 more combinations, some of which are on his website. If you’re interested in the mathematics behind the puzzles, he also has a paper laying out an algorithm to generate Shinro puzzles with desirable qualities.
The number of possible distinct Shinro games is not obvious. Orenchak claims in the introduction to his paper that there are 64 choose 12 ways to place the holes and 9^52 ways to place the arrows, resulting in over 10^40 arrangements (not all of which are valid games). Obviously, we can reduce that upper bound by identifying arrangements that are isomorphic under rotation and reflection. How small can you get that upper bound to be? Let us know in the comment section.