Legendre’s Conjecture

Posted on September 29, 2013 by Christian Luca
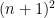Adrien-Marie Legendre (1752-1833), known for important concepts such as the Legendre polynomials and Legendre transformation, states that given an integer n > 0, there exists a prime number, p, between n^2 and (n+1)^2, or alternatively, 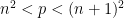n^2 < p < (n+1)^2.  This conjecture constitutes one of Edmund Landau’s
four “unattackable” problems mentioned at the 1912 Fifth Congress of Mathematicians in Cambridge.

A table of the results of the primes
that exist between n^2 and (n+1)^2 can be seen below.

n
Condition: n^2 < p < (n+1)^2
Prime
numbers, p
Number of primes between n^2 and
(n+1)^2
1
1
< p < 4
2, 3
2
2
4
< p < 9
5, 7
2
3
9
< p < 16
11, 13
2
4
16
< p < 25
17, 19, 23
3
5
25
< p < 36
29, 31
2
6
36
< p < 49
37, 41, 43, 47
4
7
49
< p < 64
53, 59, 61
3
8
64
< p < 81
67, 71, 73, 79
4
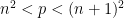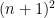We can see from the above table that indeed, the Legendre Conjecture holds true for the cases considered, with at least two prime numbers, p, fulfilling the inequality, n^2 < p < (n+1)^2.  Furthermore, the positive integers, n^2 and (n+1)^2 are referred to as square numbers.  But, how would one go about proving the conjecture true for any n?The best effort so far, it seems, was given by Chinese mathematician, Chen Jingrun (陳景潤) (1933-1996), who proved a slightly weaker version of Legendre’s Conjecture: there is either a prime, p in the interval, 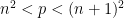n^2 < p < (n+1)^2 or a semiprime, pq, in the interval, 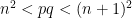n^2 < pq < (n+1)^2, where q is a prime not equal to p.  A semiprime is a composite number > 1 (not prime) that is the product of two prime numbers (could even possibly be equal primes). Examples of the initial semiprime numbers are 4, 6, 9, 10, 14, 15, 21, 22, etc. Examples of the first several semiprime numbers whose factors are distinct and for which Jingrun proved a slightly weaker version of Legendre’s Conjecture are: 6, 10, 14, 15, 21, 22, 26, 33, 34, etc. If the Legendre Conjecture turns out to be true, then the gap between any two primes, p_n and p_{n+1} would be O(p^{1/2}), where p is a prime number, and O constitutes the big O
notation.  Understanding the big O notation, let’s look at the table above for the case n = 2, for which it is found that the prime numbers 5 and 7 fall within the interval,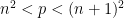 n^2 < p < (n+1)^2; therefore the gap between 5 and 7 should be 5^{1/2}  which is about 2.236.  Accordingly, the gap between prime numbers in big O notation has to be adjusted to become more representative of the actual gap between prime numbers if the Legendre Conjecture is true.This problem definitely seems hard to tackle,
but time will tell whether it will be proven, whether rigorously in analytic sense or with the aid of computers in a numerical fashion.What are your thoughts on approaching Legendre’s Conjecture?

About Christian Luca

Christian is studying at the Illinois Institute of Technology (IIT) as a distance-learning student in the Professional Science Master's program in health physics. The branch of physics called health physics concerns itself with the interactions of radiation and the environment. His hobbies include listening to classical music, and playing the piano and/or trombone whenever he gets the chance. In 2011, he married Cassaundra, and they have a beautiful, 14-month old daughter, Eliana, and currently live in Cleveland, Ohio--a great city for classical music opportunities, and the home of the Cleveland Orchestra!
This entry was posted in Math. Bookmark the permalink.

8 Responses to Legendre’s Conjecture

  1. rm says:
    December 9, 2015 at 4:47 pm

    I am not sure if it is relevant, but I have something I call silly prime tricks, where I could see the pattern of primes geometrically, and tap them out musically. y=2x+3 will intersect every positive odd number, from which you can measure the hypotenuse distance between any odd or odd prime number using the Pythagorean theorem. All odd primes Ive plugged in work. The distance between 5 and 7 is the square root of 5, which is very close to the value of the gap indicated.

  2. mahdokht says:
    January 22, 2016 at 5:33 am

    I’m an iranian student have been working for 7 months on this problem…ì acchived good results…this is not as hard as what you think…only a simple creative solution will solve it…

  3. michaelmross says:
    January 22, 2016 at 3:17 pm

    mahdokht: Do you have it?

    It’s obviously correct, but that knowledge doesn’t prove anything. For example, you only need to multiply 1/2 * 1/3 * 1/5 * 1/7… (the prime factors) to the largest prime less than half a quadratic interval to see there must be an odd (prime) deficit. That’s an application of the Euler product formula. Mathematicians know about that, and it doesn’t provide a deterministic proof to infinity as far as they’re concerned.

    After obsessing about this conjecture for a year-and-a-half, I have a solution that I’m satisfied with: https://www.quora.com/profile/Michael-M-Ross/Mathrodite/Linear-Parity-Proves-Legendres-Conjecture

    I’m guessing you’re an enthusiast – not a trained mathematician – like me. Wish you the best of luck.

  4. michaelmross says:
    January 22, 2016 at 3:24 pm

    I meant “to add 1/2 + 1/3 + 1/5 + 1/7…”

  5. Rob Taylor says:
    November 22, 2017 at 1:23 pm

    My thoughts on the conjecture are stated in my blog entry on the subject:

    https://justmathstuff.wordpress.com/2017/11/21/a-treatise-on-the-prime-numbers-including-proofs-of-brocards-legendres-and-andricas-conjectures/

  6. David Cole says:
    March 2, 2018 at 12:17 am

    FYI: Proof of Legendre Cojecture via application of PNT

    Key Result:

    π((n+1)^2) – π (n^2) → π(n) = n / log(n) as n →∞.

    Relevant Reference Link:

    https://www.quora.com/Can-we-disprove-that-for-any-positive-integer-n-there-are-at-least-two-prime-numbers-between-n-2-and-n-1-2/answer/David-Cole-146

Comments are closed.