| Page 2

Happy Pride

Posted on June 30, 2021 by Brian Katz

As Pride Month comes to an end, I few resources related to supporting queer mathematicians.

(1) A research paper by Cech and Waidzunas that asks: Do lesbian, gay, bisexual, transgender, and queer (LGBTQ) professionals face parallel experiences of disadvantage in STEM? They find that

Controlling for variation by demographic, discipline, and job factors, LGBTQ STEM professionals were more likely to experience career limitations, harassment, and professional devaluation than their non-LGBTQ peers. They also reported more frequent health difficulties and were more likely to intend to leave STEM. These trends were similar across STEM disciplines and employment sectors. We found no differences by LGBTQ status in education level, work effort, or job commitment. These findings reveal LGBTQ status as a clear axis of inequality in STEM and motivate further research into the mechanisms producing such outcomes.

(2) If you are identify as trans or non-binary, you might be interested in Trans Math Day(s): July 14-15. The organizers point out

While we greatly appreciate the support and aid of allies this event aims to center trans and non-binary people, and as such we ask allies not to attend or register, but instead use that time to do other forms of allyship work.

(3) TODOS has released a “Statement in Support of LGBTQ+ Persons”. The statement asserts that

TODOS recognizes the direct impact these [anti-transgender] bills have on our students’ physical and mental health, teachers, and others working in education. We believe that these anti-transgender bills and the discourse surrounding them, even if they do not pass, contribute to a hostile environment for LGBTQ+ persons generally and transgender persons specifically. We have a duty to oppose and counteract these measures, to speak out about these direct attacks on LGBTQ+ Persons, and to protect the well-being of our students, family, friends, and colleagues. We must stand up against transphobia, homophobia, and hate in any form against LGBTQ+ Persons.

This statement contains links to multiple other resources and ideas for action.

(4) The 2022 International Congress of Mathematicians is planned for St Petersburg, Russia, where it is defacto illegal to be part of the LGBTQ+ community. Many people feel concerns for our lives are being dismissed by those making decisions about this event. Here’s a thread about actions people can advocate for that would help.

(5) We must also stand in solidarity with Black folks, who are so often the targets of institutional violence, and Native Americans, especially in this time when the horrors of “boarding schools” in the US and Canada are finally being acknowledged for what they were in public discourse. Solidarity is vital in general, but it is also important to realize that Black and Indigenous queer people have often been the minds and actors behind movements that earn human rights for all queer people.

Posted in introduction | Comments Off

Who will celebrate you?

Posted on June 21, 2021 by Brian Katz

Guest post by Noelle Sawyer

You’ve reached the end of your mathematical career. There is a celebratory conference in your honor. Who is speaking? Who is invited?

Your career is cut short, but it was stellar. A prize is named after you. Who are the recipients?

You didn’t get your flowers while you were here, but after you die, a lectureship is named in your honor. Who is giving the lectures?

If the image you conjured in your head is a group of cis straight white men, I need you to question that. Why and how, in a celebration of you and your mathematics, are the people doing the celebrating all the same?

You may have seen or heard me say this recently, and I stand by it: If the only way you can celebrate me after I die is by giving more things to cis straight white men, then I ask that you do not celebrate me.

What is the harm to you and your legacy if a mathematician with different identities than you speaks in your honor? No, really. Ask yourself.

Some of you may be distressed at this moment. How can you be properly celebrated by any other group of mathematicians when all the best mathematicians in your field are white? They’re all men. As far as you know, they’re all cis and straight. Again, now is the time to ask yourself questions:

Are those really the best mathematicians, or are they the ones that I see the most?
Are they getting published the most because they’re inherently better, or are there politics and other circumstances to consider?
Does my mathematical circle just look a lot like me?
When was the last time I spoke to a mathematician of color at a conference?
Do I know any trans mathematicians?
Is there someone in my field who gatekeeps to make sure that ‘the best mathematicians’ always look the same?
Am I gatekeeping?

That’s just a list to get us started.

In recent weeks, I have been asking how speakers are chosen for the Maryam Mizrakhani lecture at JMM. The AMS renamed the Gibbs lecture, one of the AMS invited addresses, and held the first Maryam Mirzakhani lecture in 2020. I have been told that speakers are chosen regardless of race or gender. That the goal of the invited lectures is to celebrate excellent mathematicians. As a result, two of the three invited speakers have been white men so far.

I’ve gotta tell you: When I hear people making choices for something “regardless of race or gender” all I hear is “we’re going to pick white men and you can’t stop us.” That’s not me putting words in anyone’s mouth. That’s using my experience in life so far. Not considering race or gender very rarely works out for people who are not white men. When you do things without paying attention to color or gender, of course you can ‘accidentally’ pick a white man every time. Now is the time for questions again: Why do you think that most of the ‘excellent mathematicians’ are white men? Are there reasons that white men might be more prolific at an earlier stage of their career than others?

Should you continue that pattern by highlighting white men who are already recognized as being excellent mathematicians by their peers? Are there other mathematicians who are just as deserving, but have been given fewer opportunities to stand in the sun and have everyone see them as having value?

The AMS can do that. The AMS can give the validation that a mathematician is excellent by having them give an invited lecture at JMM. The AMS can put a mathematical stamp of approval on anyone’s CV by simply extending the invitation. So why is the AMS so worried about making choices regardless of race or gender to celebrate excellent mathematicians? You make the rules, AMS! You can make this decision. The only thing standing in the way of the AMS is the AMS.

An excerpt from an email I sent in response to finding the criteria for choosing a speaker lacking:

If the guidelines for choosing speakers do not directly address the bias with which speakers are chosen, what is the point? Why did the AMS name a lecture after Maryam Mirzakhani and not a Fields medalist from a different year? The AMS made that choice because she was the first woman and first Iranian to win a Fields medal. Now with the 2022 speaker, you are not celebrating people who are not men, people of color, or mathematicians outside of the US. Without more guidelines, the speakers will continue to be white American men, and while I’m shocked that it took until the third lecture for this to happen, I’m still disappointed that it happened at all. Again: What is the point?

The arguments I have heard about guidelines boil down to four points. Before you think these are comments paraphrased just from members of the AMS leadership, some of these are from your very own colleagues! I will answer each argument in turn:

Would Maryam Mizrakhani have even wanted the lecture named after her to have guidelines based on race/ethnicity/gender/nationality?
- This is an interesting point that we cannot answer! But also I don’t want more lectures named after people who would have an issue with this. To this I say: If you can prove that she wouldn’t have wanted this, simply name the lecture after someone else who would have.
We don’t want this to become known as the lecture that’s for women or people of color!
- The suggestion here is that reserving something important for people who are not white men will devalue it. That is, dare I say, both racist and sexist.
We’ll miss out on so many great speakers if we have fewer white men speak!
- I promise that the white men you want to invite are giving other talks. They are not being hidden away. No one is blocking their shine. However, you’re missing out on great speakers now who are not as readily invited to be plenary speakers at conferences.
We can just reserve some other lecture or prize for women of color, since you want one so bad.
- Why not this lecture? What is wrong with putting guidelines in place for one of the AMS invited addresses? Do you want to give us something less fancy? Again: Ask yourself why.

I’m going to repeat my private comments in public:

While this may be a careless coincidence, making that choice feels deliberate and malicious. Just this year, I read the report of the Task Force on Understanding and Documenting the Historical Role of the AMS in Racial Discrimination. All 68 pages. Nothing in it surprised me because I exist in the mathematical community as a Black woman. However, the report touched on this particular issue already. On page 47, speaking about the Section Program Committees: “The charge of these standing committees lacks concrete instructions on how to seek a diverse set of speakers beyond gender.” So far, the speakers for the Maryam Mirzakhani lecture have not even been a diverse group based on gender.

It’s not just about this lecture. It’s about having to see an announcement for the “Fellowship for a Black Mathematician”. It’s about not once attending a special session at a sectional meeting with more than two other people of color. It’s about the AMS repeatedly informing me and my community that it does not care enough to be careful with its choices and how they affect us.

I am asking with this ~~email~~ blog post that the AMS:

Write clear guidelines on how speakers will be selected to give the Maryam Mirzakhani lecture and include specifics about ensuring that there is representation of gender, ethnicity, and nationality.
Publicly post said guidelines.
Select another speaker for the 2022 Maryam Mirzakhani lecture.

The final question I want you to ask yourself:

Why not?

Some notes:

Since I first drafted this post, I have been encouraged to join an AMS committee. I respectfully decline. I will most likely continue to do so unless I see evidence of change happening without me there. If the wheels aren’t turning before I get there then I, Noelle the untenured Black woman mathematician, will not be spending my time trying to grease them. Instead, I have spent time sending emails which state my case and are the points I would make in any committee meeting. Really, remove the points about Maryam Mirzakhani being a brown woman herself and replace names; you could read much of this post word for word to make any argument for making changes to any named lectureship, prize, or award.

I have been told that the Prize Oversight Committee was created to work on the problem of how the AMS chooses awardees for prizes and lectureships. It has been in existence for approximately the same amount of time as Maryam Mirzakhani has had an AMS invited address named after her.

I have also been told by the AMS president, Ruth Charney, that ensuring a broader distribution of speakers for named lectureships has been specifically added to the agenda for at least one AMS committee. I hope that’s true, and I hope to see change.

[Editorial: The guest author selected the featured image to summarize the tone of this piece.]

Posted in introduction | 4 Comments

I want to quit my job part 1

Posted on May 24, 2021 by Piper

I’ve sat on this post for a while, not sure what to do. It began as a letter to my students, but it didn’t read as one. It wasn’t exactly helpful to my students and would probably just bring them more pain. It was clearly written for you all to read, but I couldn’t stop addressing the students I wished I could reach.

I started out angry. So, so, angry. But now I’m just sad. Well, tired and sad.

I hate my job.

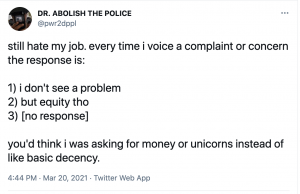
screen shot of this tweet: https://twitter.com/pwr2dppl/status/1373374900585517056?s=20

Exhibit A

Obviously if asked, in person, I will say that nothing I write is 100% accurate because I cannot in a set of coherent words express all of my feelings and all of the nuances I carry in my mind.

I want the people I work with to think this is about them in as much as I want them to think about how their actions affect others. I don’t, on the other hand, want to be accused of starting smear campaigns or going after people or being vindictive. I’m not about spite. In fact, I’m about restorative justice.

But mostly I’m about not being silenced.

a post from user Piper H, the text reads: You made Piazza unsafe for me, the only place in this course that was comfortable. Social media is how I am surviving this semester. I believe it is important not to doxx people, so if I accidentally released your name I would definitely undo that. But I will not be silencing myself to make you more comfortable. I don't know if you have attended any of the Equity Forums, but maybe that's a good place to start if you want to understand this situation better.

Exhibit B.
My response in an instructor’s only post on Piazza requesting that I remove my complaints from Twitter.

So it’s a delicate balance between truth and fiction, keeping my job, and keeping my promise to always be honest with you.

Still, I have learned many things I did not know.

I do not believe that I or any other human has the right to pass judgment on others.
I do not believe that I or any other human has the right to ask, encourage, or set someone up to sacrifice their health for capitalistic goals.
I will not accept being ignored or gaslit by my instructional supervisors, especially when I am trying to protect students.
I will not allow undue suffering of the many in order to protect the theoretical journey of a few.
If I am forced to choose between students and professors, I will choose students.
Professors routinely abuse students in the name of meritocracy and I will not agree and will not play nice and I will not cover.
The reason we have the legal right to assign as much work as we want, the reason we can roll our eyes at student excuses, the reason we can require a student to prove they haven’t cheated, the reason cheating is even a concept involved with learning, the reason it is so easy to ignore what passes for student feedback, is that we are the oppressors walking around reveling in our supremacy which we think we earned via surviving the very oppression we perpetuate.
I cannot be the good cop.

Without further ado, my not-actually-to-my-students letter to my (now, former) students.

Breathe in, breathe out. (Writing this makes me anxious; I will take breaks.)

Dear students,

I do not know exactly how to do this, because I do not want to upset or demoralize anyone who is doing okay right now. It is okay if the current system works for you. Each of you deserves to learn calculus and have a good experience. Just like I’ve met the rare person who enjoyed an emotionally unsupportive grad school, I am certain that some number of you are really into the material and are good with how it’s presented and enjoy the freedom that comes with the anonymity of remote learning. I do not want to take anything away from that. The problem is that I know that a sizable number of students are struggling. And I know that I am struggling. And I know that we are being lied to.

Think grounding thoughts… Five things I see: headphones, dinosaur, bean bag chair, ipod (yes, ipod), textbook…

Students, I have always said that you cannot trust your professors: we are people with unearned power in a system that feels no obligation to prioritize anyone’s health. Imagine deciding how much homework to assign, and all you know is how much homework you had as a student. Maybe it was awful, but look at you now! Or maybe you want to be more reasonable, but you see the results from professors who overload their students and you want your students to be just as successful. This is just a small example where we make decisions that have huge impacts on you and generally we make them off of experiences and information that literally have nothing to do with you personally. At research institutions many of us run on rumors rather than education research (maybe that sounds ironic but there are actual math professors who are paid actual money and yet don’t believe in math ed).

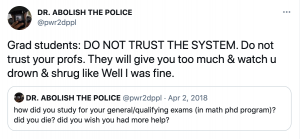
screenshot of this tweet: https://twitter.com/pwr2dppl/status/981938136484691969?s=20

Exhibit C.
In which I have been me in public for years.

That you can’t trust your professors is already known in terms of sexual misconduct data, by the way. I don’t know why we don’t talk about this. Since I’m here, I might as well tell you to Stay Away from charming professors.

Stay. Away. from Charming Professors.

Professors who allow you to think highly of them while they casually cross boundaries because they’re so comfortable with you?

Predators.

I routinely use my vulnerability as a tool to empower others, and I’ve seen that many students respond in a caring way. It is flattering, and I would love to think that we’re all just humans sharing in the struggle, but we are not. Not as long as I have unearned power over them. And I know 100% for a fact that there are professors who feed off of student admiration and concern; they will be vulnerable for a special student and that student will care about that cool professor who is sad about the thing, and that professor will use this to meet their own needs, with little regard for the harm this causes.

Abusive and toxic professors are very real and they get tenure and they keep tenure and the system just keeps going and we let students in and we know it’s not safe. Abusers get grants and give public addresses and sometimes they organize workshops on diversity and inclusion.

Being employed by a top university does not mean someone is a worthwhile person. Being allowed to hold office hours for students does not imply this is a person a student should ever be alone with. And it’s going to stay that way for as long as universities have a conflict of interest between status and education.

But I digress.

Rihanna dancing on stage with arms crossed, text: STAY MAD

Me when profs get mad that I am honest with students about my concerns for their well-being.

If your university and your professors won’t keep you safe, who will? How can you tell if you’re being appropriately challenged or merely exploited?

I have no idea. We keep you at a disadvantage. No part of the traditional North American education gives you the tools necessary for critically assessing what a teacher or professor is demanding of you. Furthermore first year students are often told repeatedly that they don’t know what college is or should be. To paraphrase a student’s retort to this attitude “is this not a first year class? Who else would be the main group to offer critique of this course?” In fact, I have no idea how we decide if a first year course is good. Do we care about students who are only with us for a year? To be honest I can’t say that there is much evidence that any of the (R1) math departments I’ve been in care about how any of our students feel if that isn’t coupled with unsatisfactory numbers. Which is to say, I’ve seen no evidence that they care about how students feel.

students in masks, social distancing, wearing signs saying UAW on strike

Now feels like a good time to advertise unions. Collective bargaining and protest are the only ways I know to give power back to the people.
Photo credit Mary Inhea Kang

Four things I feel: the bed, the keyboard, a metal nightstand I ordered online thinking it was wood, my hoodie…

Here’s the thing. I really want to talk about what we’ve been put through this semester. The syllabus, the website, the course design, the mixed messages, the don’t email your professors, the typos, the bad problems, etc. I have been so unhappy with so many aspects of the course. Yet, when I talk to my friends, I realize it’s not that any one thing in particular is so bad or unforgivable. It’s more like things are bad in multiple ways that coalesce in potentially devastating ways for some number of students. The only thing I know for sure that was missing was heart.

Lucille Blooth from Arrested Development looking at Michael. Text: I don't know who that is, and I don't care to find out.

What it’s like bringing up one student’s concern in a course of eighteen hundred.

I wasn’t sure how to discuss the course publicly in a “safe” way. Fortunately, a friend sent me a seemingly anonymous article titled Contrarian Decisions in Online Teaching [1], which I will quote from below. My intent here is to share some of the attitudes I faced and frankly could not fight. My hope is that these attitudes will stop passing as acceptable and maybe this discussion will give you the confidence to demand better, or at least to know you deserve better.

Like all other course coordinators preparing my calculus course for online delivery was my life during the summer of 2020: every decision was carefully considered, thoroughly researched, and discussed. I became well-versed in the research, conversations, and recommendations for teaching online. In the end, however, I made a few decisions that went against what are seen as common “best practices” for teaching online.

This excerpt from the introduction sets the tone. At face value it sounds great. This person did a lot of research. I love research! The last line indicates that the author went against that research, so one would hope for an understanding of why general “best practices” did not fit the author’s specific situation. Instead, we get a controlled narrative in which the author is telling us to trust them. I’ve gone back and forth about whether the article is about the author’s personal journey or about the pedagogical choices they made. Either way, this journey does not contain the research, the context, or how to evaluate these choices. The intro tells us that the author’s views and choices are to be trusted because of all the energy the author put into it. As if the decisions only impact the author and not potentially hundreds or thousands of students.

From the section “Synchronous Lectures are Not Recorded”:

Many teaching and learning centres (at least in Ontario) recommend recording synchronous lectures so that students can watch them if they are in a different time zone or if they have issues that prevent them from attending live. Along with the other first-year calculus instructors I decided not to offer lecture recordings (except for cases of academic accommodations) because of the way classes were designed.

I believe that these recommendations assume that the online class experience is pretty comparable whether you watch it live or at a different time. Our classes, however, are largely built around student activities …

While it would be very easy to post a video recording we wanted to send this message to students: your contributions to class matter.

Maybe this is a well-known rhetorical device. The bait-and-switch? The deflect-and-respect? At any rate, let’s dive in.

The premise:

Under COVID restrictions, we may no longer assume all students can attend synchronous lectures. It is recommended that lectures thus be recorded so that students who cannot attend may still benefit.

The decision:

Synchronous classes will not be recorded.

The rationale:

Recordings cannot replace live lectures given the design of the course (for instance, a flipped classroom scenario)

The last word:

We want students to know they are valued.

I banged my head against this tactic for months. There is a stated problem “not all students can attend live lecture” and there is the suggestion “we should record lectures.” This suggestion is rejected not because there is an alternative solution for students who cannot attend, but because such a decision would violate some kind of sanctity of something. The fact that recordings cannot replace live lectures is meaningless to students who can’t attend. The reason we are throwing away the concern for those students is because of the group of students who could attend, but might not if they felt like they had the choice. It is more important to restrict student’s choice than to support students who are already at a disadvantage. And then the last line is manipulation. It means you can’t possibly argue. Am I saying I don’t want students to think their contribution matters? That’s not very inclusive!!

From the conclusion:

As with most decisions that come down to following your beliefs over popular opinion I received criticism, most aggressively from others at the University who worked with students but did not take time to understand the context of my decisions. The critics assumed that I didn’t know enough about online education or that I was not thinking about the interests of students.

This is yet another thing I’ve come up against, and is a common tactic of people refusing to dismantle their own privilege: a complete dismissal of the existence of valid complaints. An assumption that critics are merely insulting/attacking/devaluing/undermining the person in charge, rather than looking at how students and/or marginalized mathematicians are impacted.

How do we face this?

A question I have asked the chair of my department is what can an instructor do if they feel that students are being mistreated by faculty? I don’t have an answer. What can a student do if they feel mistreated? If they aren’t personally targeted, if they are suffering anti-student oppression? Probably not much. I mean sure, you can complain. Tell your TA, tell your instructor, tell the chair. Is there anyone able to care? To help? What if the problem is the conscious decisions made by experienced teaching stream faculty? What then?

It is hard for me to fight course designs and pedagogy. I am not an expert in either. My experience is limited. My interest, if I’m honest, is limited. I am however an expert on being mistreated, neglected, manipulated, and made to doubt myself. I am an expert on struggling to accomplish things I “should” be able to do. I am an expert on being told explicitly and implicitly that I am not wanted in math.

When I see that happening to my students I am going to fight for them. Period.

I learned this semester I cannot work with people who refuse to value all students.

Three things I hear: my laptop trying too hard, a child asking for food, breathing…

I sat on this letter in part because I felt it was important to detail what I had to endure… but I also felt strongly it was not safe to do so. Now that the semester is over I can more easily prioritize and summarize what I want to describe.

When a student misses a deadline and emails me to accept something late, what I think about is how I have no childcare and no help and how I have anxiety and no therapy, and how I can go hours without being reminded of a deadline or scheduled event. When students are told they have to attend a synchronous lecture or live office hours, I think about all of the talks I’ve declined because I cannot commit to anything live while I am without childcare. I think of all the meetings I’ve been forced to attend and how awful it is when a child is having a meltdown while I am really trying to say or hear something. You may say you do not mind interruptions but you were never my concern.

My child does not consent to being ignored for an hour while in distress, and I can’t think properly when I’m constantly interrupted. We can’t just pretend that working from home is merely a change in location.

Two things I smell… okay, is this real? Are people always surrounded by smelly things or am I supposed to sniff nearby objects? I chose to sniff my coffee and I have zero regrets. Also leftover muffin. I’m going to go back to the coffee, if that’s okay.

In the days since my duties ended I have been unpacking the trauma of how I was treated. Usually when teaching ends I’m excited to take a break and then dive into research. That’s not where I am at. I’m still processing how little I mattered to anyone. How little you, the students, mattered. How the existence of students succeeding rendered meaningless any suffering from a “minority” of students. When a real person’s suffering is dismissed as anecdotal, I just really question the morality of remaining in this system.

My experience this semester was that instead of having my needs accommodated, I was condescended to. My energy was demanded. I was told that they knew of my writing and they wanted me to fight for the students. They wanted me to challenge them, but only on their terms. I was asked to do things I couldn’t and when I explained that I couldn’t, I was made to feel bad.

One thing I taste, guess I’ll go with coffee again…

Students, nothing is more important than your physical and emotional health and safety. No calculus course is going to be designed to meet everyone’s needs. If a course is failing to meet your needs, that is the course’s fault. Learning should be wonderful! Life in a pandemic is hard. Being isolated is hard. It’s not fair. None of this is fair or right or just. My personal opinion is that we should have thrown out everything and focused entirely on communal support. But then again students need degrees and jobs and none of us can put everything on hold. But I wish the judgment and cruelty in education would finally die. I know that standing up for yourself and demanding more is a risk. I am not someone who can organize a student strike or even design a better course.

I can only tell you that you are being mistreated. I know it because I have been mistreated. I can only tell you that you are being disrespected. I know it because I have been disrespected.

screenshot of this tweet: https://twitter.com/pwr2dppl/status/1379907439173177347?s=20

How do we make sure victims are heard in a culture that hates discomfort and fears accountability?

Some day I hope to be able to talk about it more openly.

For now, I leave you with a few well wishes to all the students out there from some educator friends:

“This system is obviously, horrendously, and in every way that matters, failing you. Some of that is beyond our control. Some of it isn’t, and for that, we need to do better because we owe it to you. Not as customers but as people.”

“You matter more than this class. Your mental health, your access to material resources, who you love, what you enjoy should not be sacrificed ever. You have a right to be a human first and a student second. You should be trusted to do your work in community with us.”

Sincerely,

Prof H

1. I have been informed that the post doesn’t show up on search engines, so I am including the link here, but please only comment/engage with that post if you are supportive of it. Any critique of that post should stay here please.

Feature image taken from: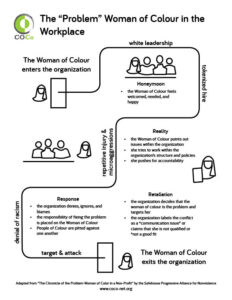

Posted in equity, inclusive pedagogy, mathematics experiences, mental health, racism, social justice, supporting students | 5 Comments

Women of Color: Who Tells Their Stories? (and why it matters)

Posted on May 3, 2021 by Brian Katz

Guest post by Courtney Gibbons

The AWM EvenQuads deck is a lovely idea. Bringing more women in mathematics into the spotlight is a laudable effort. To be sure, the intention deserves recognition.

However, it is also necessary to recognize that the outcomes are not universally positive.

Continue reading →

Posted in introduction | 3 Comments

Amplifying Excellence

Posted on February 22, 2021 by Brian Katz

I wanted to amplify some recent and ongoing excellent work and news!

Mathematically Gifted & Black

Mathematically Gifted & Black (https://mathematicallygiftedandblack.com/) continues to share exceptional profiles of mathematicians every day this month. MG&B is organized by Dr. Erica Graham, Dr. Raegan Higgins, Dr. Candice Price, and Dr. Shelby Wilson.

You can follow MG&B on Twitter, Instagram, and Facebook. You can also contribute to their effort to support the next generation of under-represented minorities in mathematics (https://mathematicallygiftedandblack.com/support/).

A profile of Dr. William Claytor

In late January, Dr. Ranthony A.C. Edmonds authored and shared a Twitter thread about Dr. William S Claytor. As many others have noted, Dr. Edmonds’s thread is expertly researched and written. Dr. Claytor was “an outstanding black mathematician” who “would have greatly benefited benefited consistent support of the mathematical community”. And as others have noted, Dr. Claytor is obviously worthy of having a fellowship named in his honor.

The Hesabu Circle

Dr. Kagba Suaray “wanted to create a space for the Black community to connect with each other and meet others with a shared interest in math”, so he joined with Robin Wilson, Edray Goins, Kyndall Brown, Rob Rubalcaba, Pamela Lewis, Micki Clowney, and Kekai Bryant to create the Hesabu Circle, “named after the Kiswahili word for mathematics”. As described in the Facebook group, the Hesabu Circle is a space created by black mathematicians & educators where black students “from pre-K to post-doc” can connect with each other & faculty, and rediscover our innate excellence in the mathematical sciences.

You can follow the Hesabu Circle on Facebook, Twitter, and Instagram. And you can read more from Dr. Suaray in recent articles from CSULB and a Long Beach community paper.

New NAM Leadership

The National Association of Mathematicians has recently had an election for President. I want to thank Dr. Edray Goins for his years of service, and Dr. Leona Harris for her work as Interim President, and I’d like to congratulate Dr. Omayra Ortega as the new President!

You can follow NAM on Facebook and Twitter. You can join NAM as an individual or institution and donate to NAM’s efforts.

Posted in history of mathematics, mathematics experiences, minorities in math, racism | Comments Off

The mathjob market is bad. But what else is new? A 2020 retrospective

Posted on February 1, 2021 by Tian An

Let me start by saying that it’s no news to anyone that the pandemic has affected the academic job market. At the same time, it’s nice to have some data to back up that feeling of doom. Especially for someone like me, who had been on the job market every year between 2015 and 2019 (would not recommend, in case you were wondering), I constantly heard that the job market was tough. But if it’s tough every year, what’s the difference?

In early October 2020, Science reported about a 70% drop in US job postings on their job board, a pretty drastic number. On the other hand, since US math jobs appear primarily on mathjobs.org, and plus the fact that the economy has made an impressive (and frankly, unequal) recovery since the initial crash in March 2020, maybe it’s worth taking a closer look at how the pandemic is affecting math jobs.

So how bad was the 2020 mathjob market?

Going into 2020, the number of graduating PhDs in Mathematics, Statistics, and Biostatistics had been steadily on the rise, a number that the AMS tracks very well.

On the other hand, the number of jobs posted appeared to be relatively stagnant, between 2013 and 2017, as documented by the AMS again,after which time there was a slow rise in job postings on mathjobs.org, as the graph below shows. When the pandemic hit the US in March 2020, freezing the job market, we saw an initial decrease in job postings (and not to mention a drop in employment which isn’t measured here). Continue reading →

Posted in cultural pressure in academia, equity, graduate school, minorities in math | 2 Comments

Oh my heart

Posted on January 15, 2021 by Piper

You’ve broken my heart for the last time.

That’s what I want to tell white America, but I know it’s not true. My heart will be broken by you over and over and over again before I die.

You’ve broken my heart for the last time.

That’s what I want to tell academia, but that will only be true if I quit (maybe), and on that I am still undecided.

What happens when people are given an enemy?

They show up armed.

Armed Militia at the Michigan State Capitol April 30, 2020
Photograph: Seth Herald/Reuters

Whether the enemy is a box of ballots, a Congress tasked with counting, a police officer who actually wants to protect, or human beings seeking equity after generations of trauma and loss.

In early 2008 I was swept up in the grassroots movement sparked by the Obama campaign. His message of hope and change resonated with me in a way that will probably never happen again. One of his messages was that we are all basically the same. We may have ended up on different sides of certain politicized debates, but there’s more that unites us than divides us.

Well, with all due respect to my younger self, we cannot all be basically the same.

You’ve broken my heart, oh my heart, never for the last time, with your fear and your walls and your refusal to tie your freedom to mine.

Person wearing “Camp Auschwitz” hoodie at Capitol Hill, Jan 6, 2021
Photo credit: Andrew Caballero-Reynolds / AFP Images

No. You may not stand next to me.

The difference between self-centered cynicism and vulnerable compassion may seem small or academic, but the ramifications are too huge to sidestep with calls for unity.

Those who continue to refuse to hear what #BlackLivesMatter and abolition are all about will probably be shocked to learn that today’s broken heart, tear streaks, and inability to eat are the result of reading and watching violence against police officers attempting to protect the Capitol and its occupants from a violent coup.

On January 6th, 2021 the Capitol Police were not the aggressors, despite knowing that angry people were flying to DC for a huge protest against what Congress was about to do. That those people were not met with riot gear speaks to the very double standards #BLM activists protest. There’s a lot we still don’t know about what happened and why, but videos and testimonials have come out painting a much darker, more violent image than what I saw shared on social media when I was supposed to be attending a JMM session.

AMS MAA Joint Statement of thoughts and prayers

I need you to know that the fascist, anti-democratic, racist nature of the rage at the Capitol taints everything it touches. I need you to know that it matters whether you are angry at a cop because they are a source of terror or because they are protecting democracy. You can tell it matters because this crowd held Blue Lives Matter flags while beating a (white) officer to death.

Capitol Hill, Jan 6, 2021
Photo: Zuma press / eyevine

I need you to know that there’s a difference between wanting justice and wanting what you think someone owes you personally.

I can’t eat because I keep thinking about the Black officer who is a part of a racist system but on this day was a human being facing a throng of rage and it was his job to protect the Capitol, and the people who were supposed to support him weren’t there. The system he bought into wasn’t there to back him up. He was betrayed by white colleagues. He was spit on and called racial slurs by out-of-town officers. And when it was over, he was alive, and he cried and yelled for all to hear.

Why should that affect me so? Why bring this to the attention of the math community? (Aside from the fact that Every Single Time I can’t do research because of white supremacy I believe I have the right to take up white mathematicians’ time with it.) Perhaps it is because I am also part of a racist system.

Academia.

And trying to abide by the system didn’t protect me. And being a good colleague doesn’t protect me. And now that I’ve cried, I need to yell for all to hear.

As I watch the slow reckoning (maybe) unfold, seeing who sides with sedition and who sides democracy, I keep thinking about how much those people really just hate Black folks. Those insurgents were as ugly, as angry, as disrespectful, as arrogant, as dangerous as anything I’ve seen and all for a widely discredited failed leader. Yet they see Black and Brown and Queer communities standing up in righteous anger (with medics, and water, and music) and they see something to step on, to squash. It isn’t rational. “We’re doing this for you” said a Blue Lives Matter rioter while assaulting a cop.

That Black officer and I are on two different sides of a certain politicized debate but we have a common heartache—that feeling when you realize they don’t see you. You aren’t a friend or colleague or officer of the law anymore, you are a threat. And they would rather beat you down than be vulnerable and interrogate their own violent tendencies. We share the heartache that comes with investing in a system you’re told will protect you, only to find the opposite is true. We share the need to do what we think is right, even if it benefits our oppressors, even if our colleagues will never understand how much it hurts.

“LET EMPATHY BE YOUR NEW NORMAL” sign
White Coats for Black Lives, June 20, 2020, Central Park, NY,
Photograph: Maria Khrenova/Tass

We are not basically all the same, but the difference is not in what we look like, whether or with whom we fall in love, or which lands our ancestors most connected with; the difference is a choice to fully embrace all of humanity, or to do anything less. Because anything less than full acceptance of all that humankind has to offer leaves you open to believing lies tailored to make you see enemies where you could have seen potential allies. We are currently bearing witness to the fatal cost even one big lie can bring.

Contemplating how a big lie coupled with insecurity (economic or otherwise) can poison someone, I turn my mind to mathematics and to academia.

The big lie is meritocracy, the enemy is diversity, the weapon varies.

For some time I’ve been wrestling with my place, not in academia, but in working towards a just world. I never thought I would devote so much of myself to such a cause but I need my heart to stop breaking.

The purpose of research, generally speaking, is to further human knowledge. We must ask, though, to whose benefit? Certainly we don’t all benefit equally (or at all) from such applications of our work as predictive policing and surveillance. Furthermore the practices and norms of academia are in no way required for expanding our knowledge. If we fully embrace all that humankind has to offer, and look to the history of what gets called academic research, we will readily find our system wanting.

August 24, 2020 @themarkup

If participating in academic research makes me complicit in an oppressive hierarchy which continues to promote racism, sexism, and settler colonialism (along with all the other oppressions), at least I am an educator, you might say.

Again I ask to whose benefit?

If the people in my own community do not benefit from my PhD, who does? And if the career path of academia prevents me from being in a community I know, who benefits? If we fully embrace all that humankind has to offer, it is clear that at every level in every location the American system of education is failing, and that meritocracy is a fantasy. While college professors may be quick to say it’s too late by the time kids are college age, we can’t forget how many bad decisions at each level of a child’s life is based on teachers’ and parents’ perceptions of college admissions. Colleges and universities can change this. Privileged universities can take the lead.

When I look to the history and I look at the present, I have an incredibly hard time justifying academia on anything other than legacy grounds (which, I shouldn’t have to tell you, are no grounds at all). I must admit to be an abolitionist, but abolition does not mean just living the same life but without prisons or, in this case, universities. It means trying to imagine what a world could be like without policing, detention, and in this case without financially backed hierarchies lording over who learns what and how.

I don’t know how we do it, but I’m tired of playing the part Black colleague/committee member/panelist whose voice will be silenced or amplified depending on the audience but who is ultimately trying to save a system that is fundamentally oppressive. To be clear, nobody was on the side of Black people on January 6th. The fascist attack had me praying for Law and Order to save Democracy, but it’s a democracy that has always taken me for granted.

Capitol insurrection on January 6, 2021. (Evelyn Hockstein / The Washington Post via Getty Images)

It is time to know with whom you align yourself. It is time to recognize those who are one scare away from justifying, if not outright committing, violence against us. I need you to recognize the danger in the tenured white man prof who says he feels “this department has been good for women” while explaining why we shouldn’t hire one. Before someone gets hurt, not after. It’s hard to break out of the socially acceptable position of peacekeeper. It’s hard to look behind the veneer of someone who hoards power without much obvious effort. You must, though. Somehow. Because honestly the weakness of those who are on my side but say nothing hurts more than the overt racism.

Soon the Trump nightmare will be over, they say, but thousands will still die daily of covid, most of the insurrectionists will still have their jobs, and the country will continue to offer only piecemeal, conditional, risk-free support to Black people.

The End.

Some links:

https://www.cnn.com/2021/01/07/us/police-response-black-lives-matter-protest-us-capitol/index.html

https://www.buzzfeednews.com/article/emmanuelfelton/black-capitol-police-racism-mob

https://www.bbc.com/news/world-us-canada-55623752

https://www.propublica.org/article/no-one-took-us-seriously-black-cops-warned-about-racist-capitol-police-officers-for-years

https://abolitionjournal.org/frontpage/

https://time.com/5886348/report-peaceful-protests/