What is a Manifold? (5/6)

In our last post, we invented a new geometry by re-scaling the inner product of the usual Euclidean plane. This modification did not change any of the angles in our geometry, in the sense that if two curves intersected in a particular Euclidean angle, then in our new geometry they still intersected in the same angle. However, distances and areas had shrunk and had done so significantly at points away from the origin. For instance, we found that the total area of the plane under our new metric was – a finite value.

The plane with the new metric is, in effect, exactly the 2-d sphere (with the north pole removed). The way I had come up with the appropriate scalings was by looking the stereographic projection from the north pole of a sphere and by requiring lengths of curves on the plane to be equal to the lengths of their corresponding curves on the sphere. (For instance, a line through the origin corresponds to a great circle through the two poles.) Other interesting geometric objects which can be obtained from the usual Euclidean plane by modifying its geometry include the hyperbolic plane.

Now let’s see if this example provides enough intuition to arrive at the definition of a 2-d manifold. Imagine the shell of an ovoid in . This is a very geometric object: one can measure lengths of curves which live on its surface, calculate the areas of different regions, and so on. In fact, developing tools to solve these problems are the subject of most introductory calculus courses. However, our goal is to give these notions meaning without any explicit reference to . We want to endow the ovoid, our manifold, with an identity of its own, independent of the ambient space .

Thanks to our extended examples, we have a clue. From far away, the ovoid does not look like a plane at all. But if we fly very close to its surface, it does look very similar to parts of a plane. Mathematically speaking, we can bijectively map a piece of the manifold onto a domain in the plane:

$$\phi : V \longrightarrow U \subset \mathbb{R}^2. $$

To cover the whole manifold, we need many such mappings.

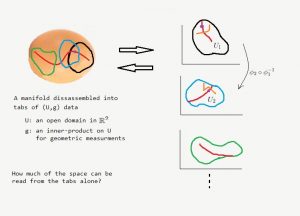
Thus, we have disassembled our shape into (probably many) separate tabs of data, each of which involves a region in the plane along with a new inner product – a way of measuring angles and distances in that region.

Now, the question is: given only the tabs, how much of the shape can we reconstruct? Can one differentiate an ovoid from a sphere by only looking at their disassembled versions? This, of course, depends on how much geometric information we record in those tabs.

Before proceeding any further, however, there is a crucial issue we have to deal with. Assume we have a curve contained in one of the regions from our tabs. Part of the corresponding curve on the manifold may cross into another region as well. Now, the image of this segment in the other tab may look nothing like a curve. (Compare the images of the orange curve under two tabs in the above picture.) The way out of this is to put requirements for the transition maps that describe the correspondence between regions from different tabs. In the above picture, the transition map that sends the orange curve in to the one in is . If we require this map to be then the image of the orange curve must be in as well.

These conditions on the transition maps will be key to our definition of a manifold. We will be able speak of “derivatives of real functions on the manifold” only if the transition maps are differentiable. We can talk about smooth maps or curves on the manifold only if the transition maps are smooth. (Notice that smoothness and differentiability do make sense for transition maps, because they are maps between open subsets of . However, for the same notions on manifolds, we need definitions.)

Next post, we will see the definition of a (Riemannian) 2-d manifold. Meanwhile, please comment your thoughts!