A few months ago, I stumbled on Tai-Danae Bradley’s excellent blog Math3ma. Bradley is a math graduate student at CUNY, and she writes about the kinds of topics that show up in first-year graduate courses and later on the qualifying exams. In her “about” page, she writes,
Math3ma was originally created as a tool to help me transition from undergraduate to graduate level mathematics. Quite often, I find that the ideas of math are hidden behind a dense fog of formalities and technical jargon. Much of my transition process has been (and still is!) learning how to fight through this fog in order to clearly see the ideas, concepts, and notions which lie beneath. Throughout this process, I’ve found that writing helps immensely.
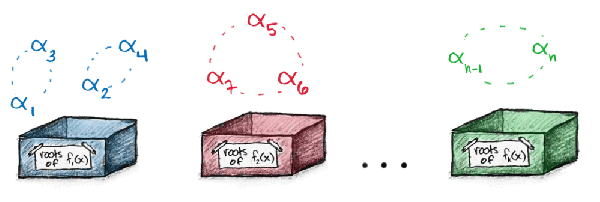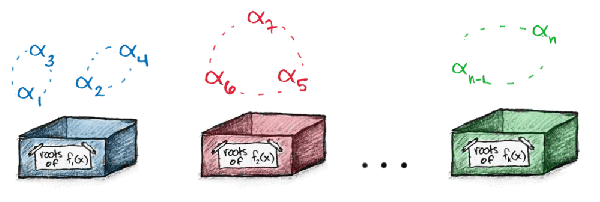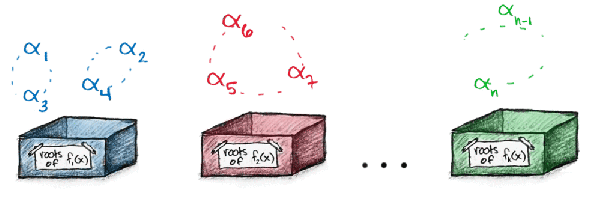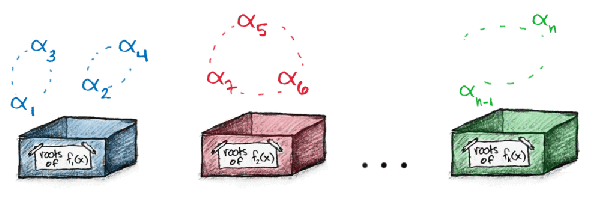
Math3ma would probably be a helpful study aid to a first-year graduate student or a nice preview for someone getting ready for graduate school. The posts include topics from first-year analysis, algebra, and topology, from Lebesgue and Borel Measurable sets to simple and non-simple groups to connectedness. I’ve been thinking about open sets recently, so I especially enjoyed her post about why open sets are everything. (They really are!) Her introduction to Galois theory is a nice overview and includes a suggestion for an abstract algebra TV commercial tagline. “Groups: it’s what they do.”
An illustration of the Galois group. Image copyright Tai-Danae Bradley.
In addition to the main posts, keeps a few tidbits in her back pocket: an unspoken rule of algebra (Stuck? Try the first isomorphism theorem!), two ways to be small, and other helpful morsels.
All of Bradley’s posts can help students get from the “OK, I understand the words in the statement and proof” stage to the “how does this fit into the big picture” stage. For me at least, that is one of the biggest challenges when learning new math. In my first algebraic topology course, it took me a couple months to realize that the fundamental group wasn’t just something we defined in passing but a major focus of the subject. (In retrospect, the word “fundamental” should have tipped me off.)
Reading Math3ma, I wonder whether my first year of grad school and qualifying exams would have been easier if I had started blogging a few years earlier! A blog like this definitely would have made a good resource when I was studying for quals. I’m looking forward to reading more from Bradley as she advances in grad school and her career in math.