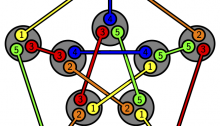
Golay Code
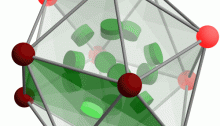
The extended binary Golay code, or Golay code for short, is a way to encode 12 bits of data in a 24-bit word in such a way that any 3-bit error can be corrected, and any 7-bit error can at least be detected. The easiest way to understand this code uses the geometry of the dodecahedron, as shown in this image by Gerard Westendorp.