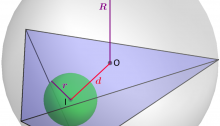
Grace–Danielsson Inequality
When can you fit a tetrahedron between two nested spheres? Suppose the radius of the large sphere is R and the radius of the small one is r. Suppose the distance between their centers is d. Then you can fit a tetrahedron between these spheres if and only if the Grace–Danielsson inequality d2≤(R+r)(R–3r) holds. This was independently proved by Grace in 1917 and Danielsson in 1949. But Antony Milne has found a new proof of this inequality using quantum information theory!