Escudero Nonic \(Q_9\) – Juan García Escudero

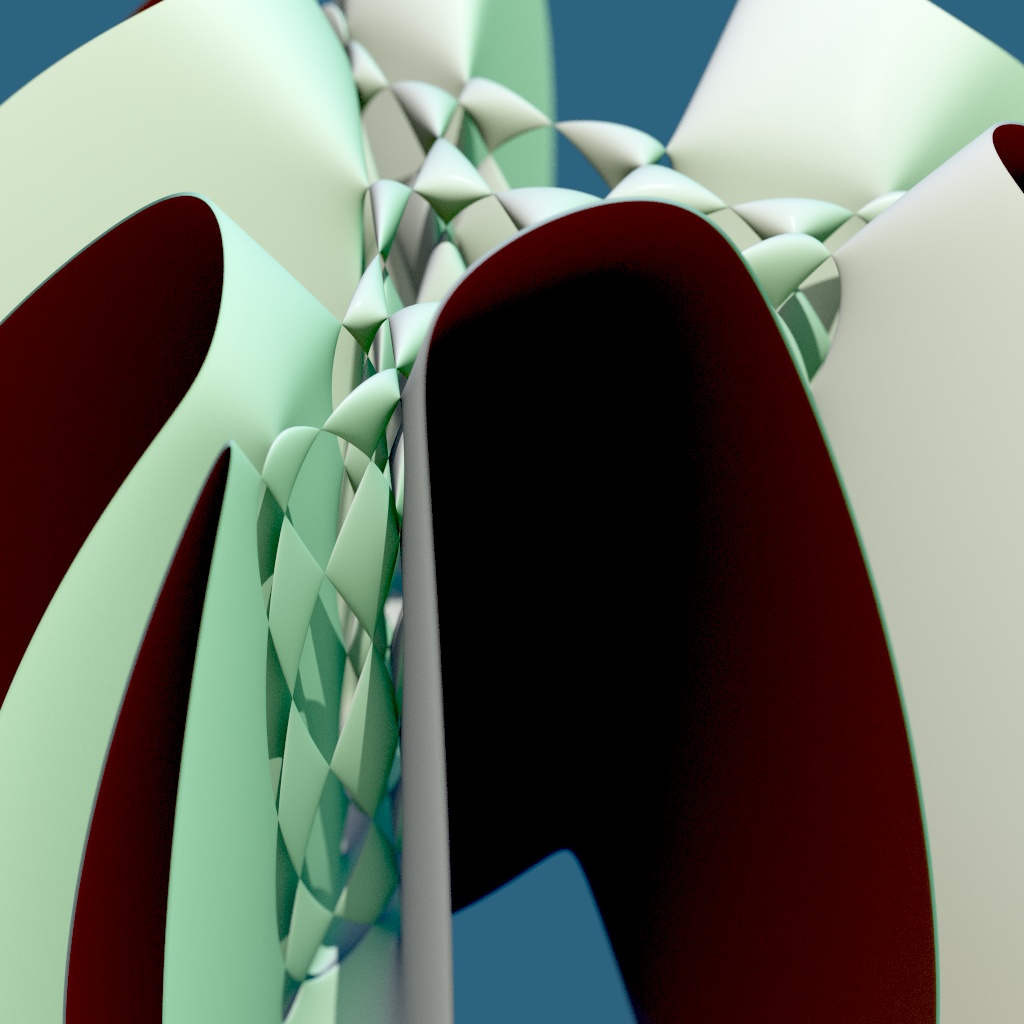
A nonic surface is one defined by a polynomial equation of degree 9. This image by Juan García Escudero shows a nonic surface called \(Q_9\), which has 220 real ordinary double points: that is, points where it looks like the origin of the cone in 3-dimensional space defined by

$$ x^2 + y^2 = z^2 .$$

Here are some other pictures of this surface, made by Abdelaziz Nait Merzouk:

Escudero Nonic \(Q_9\) – Abdelaziz Nait Merzouk

Escudero Nonic \(Q_9\) – Abdelaziz Nait Merzouk

Escudero Nonic \(Q_9\) – Abdelaziz Nait Merzouk

In 1983, Varchenko showed that the maximum number of ordinary double points for a complex nonic surface with no other singularities is ≤ 246:

• Alexander N. Varchenko, On the semicontinuity of the spectrum and an upper bound for the number of singular points of a projective hypersurface, J. Soviet Math. 27 (1983), 735–739.

These double points might or might not appear in a real form of the surface. In his 2005 thesis, Labs described a nonic surface with 226 complex nodes:

• Oliver Labs, Hypersurfaces with Many Singularities—History, Constructions, Algorithms, Visualization, Department of Mathematics, Johannes Gutenberg University of Mainz, 2005.

but not all these are real. In 2008, Breske, Labs and van Straten showed how to construct a nonic with 216 real ordinary double points:

• Sonja Breske, Oliver Labs and Duco van Straten, Real line arrangements and surfaces with many real nodes, in B. Jüttler and R. Piene, eds., Geometric Modeling and Algebraic Geometry, Springer, Berlin, 2008, pp. 47–54.

The largest known number of real ordinary double points for a nonic surface with no other singularities is currently 220, obtained by Escudero:

• Juan García Escudero, A construction of algebraic surfaces with many real nodes, Annali di Matematica 195 (2016), 571–583.

In addition to the surface \(Q_9\) shown above, he found and drew another, called \(\tilde{Q}_9\):

Escudero Nonic \(\tilde{Q}_9\) – Juan García Escudero

Both of these are defined using Chebyshev polynomials and arrangements of lines related to substitution tilings. The technique works more generally to provide surfaces of degree \(3n\) with many real double points. See his paper for a picture of a degree 12 surface with 582 real double points, and a degree 15 surface with 1162.

Abdelaziz Nait Merzouk created three pictures of the Escudero nonic \(Q_9\) and made them available on Google+ under a Creative Commons Attribution-ShareAlike 3.0 Unported license.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!