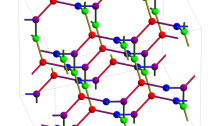
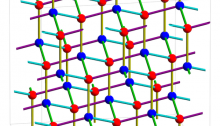
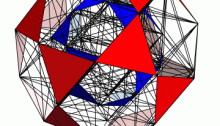
Laves Graph
This picture by Greg Egan shows the Laves graph, a structure discovered by the crystallographer Fritz Laves in 1932. It is also called the ‘K4 crystal’, since is an embedding of the maximal abelian cover of the complete graph on 4 vertices in 3-dimensional Euclidean space. It is also called the ‘triamond’, since it is a theoretically possible — but never yet seen — crystal structure for carbon.