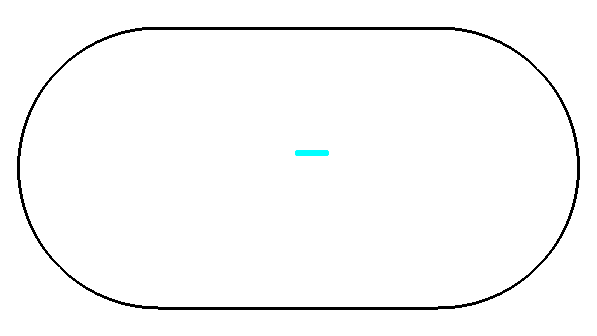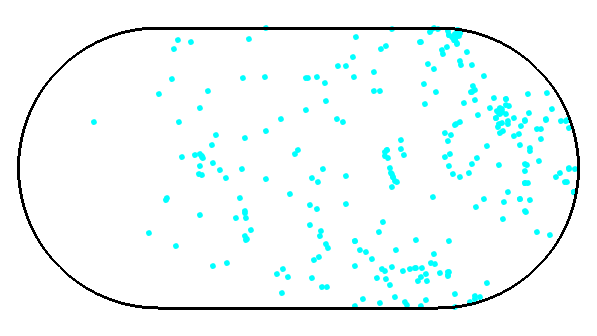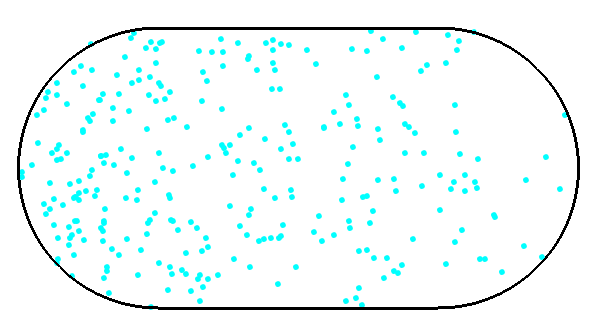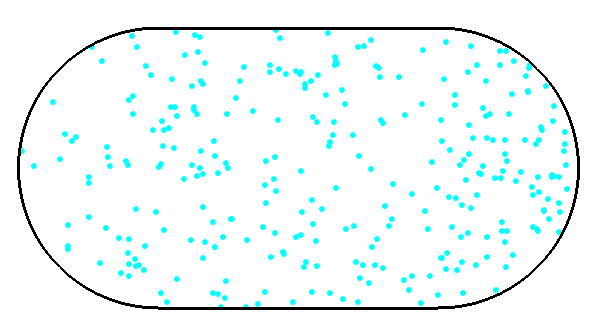
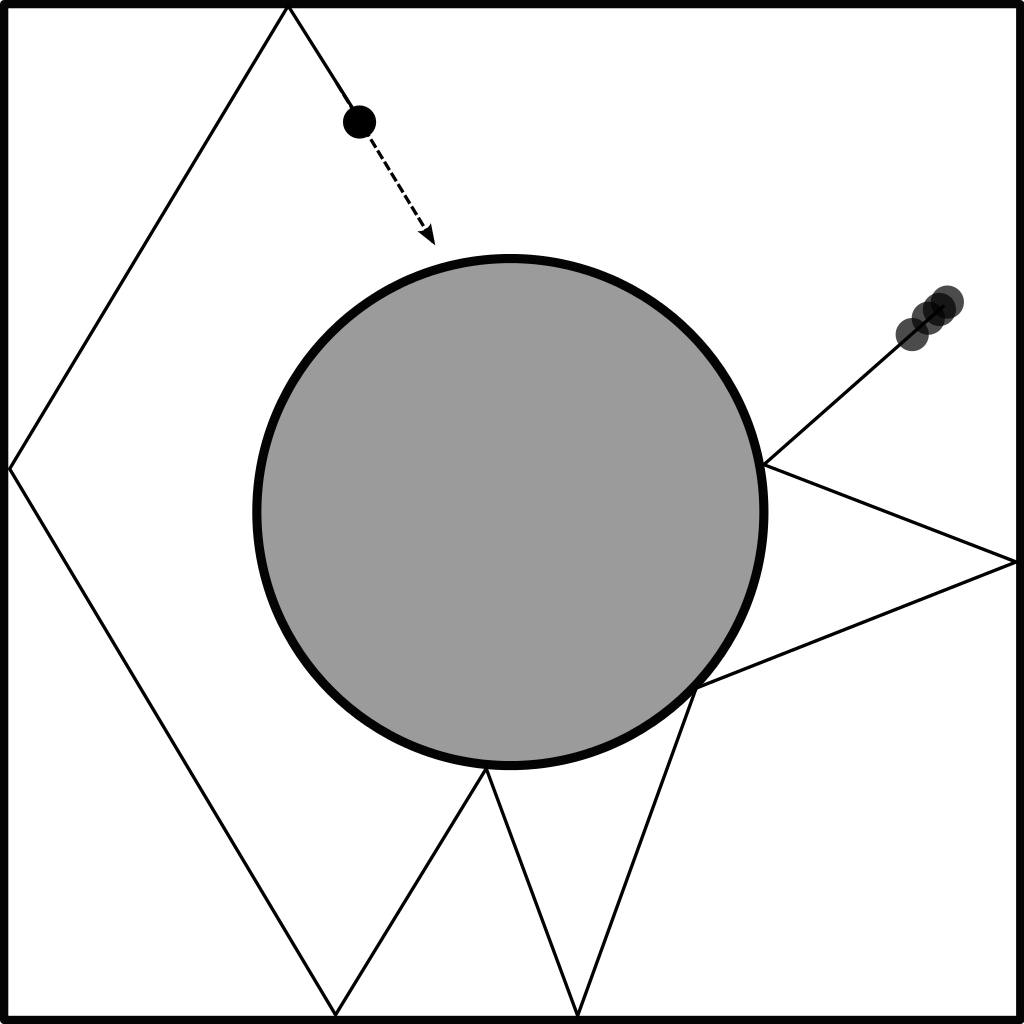
The Bunimovich stadium is a rectangle capped by semicircles in which a point particle moves at constant speed along straight lines, reflecting off the boundary in a way that the angle of incidence equals the angle of reflection. This animation, made by Phillipe Roux, shows a collection of such particles initially moving in the same direction. With each bounce their trajectories diverge, and after a while they are distributed almost evenly through the whole stadium, though for a while one can still see a density wave moving back and forth.

The Bunimovich stadium appears in the 1979 work of Leonid Bunimovich:

• Leonid A. Bunimovich, On the ergodic properties of nowhere dispersing billiards, Commun. Math. Phys. 65 (1979), 295–312.

He showed that the motion of a billiard in this stadium is ‘ergodic’. This is a way of making precise the intuition that given a billiard with randomly chosen initial position and velocity, over time its position almost surely becomes uniformly distributed over the whole stadium.

More precisely, we can define the phase space \(\Omega\) for the Bunimovich stadium to be the space of position-velocity pairs where the velocity is a unit vector. (Since the speed of the billiard does not change, we may assume it is normalized to 1.) There is a probability measure on \(\Omega\) for which time evolution defines measure-preserving dynamical system:

$$ T_t : \Omega \to \Omega , \qquad \qquad t \in \mathbb{R}. $$

Given a measure-preserving dynamical system, we say a measurable subset \(A \subseteq \Omega\) is invariant if for all \(t \in \mathbb{R}\) the sets \(T_t(A)\) and \(A\) differ only by a null set, meaning that the symmetric difference \(T_t(A) \triangle A\) has measure zero. A measure-preserving dynamical system is ergodic if the only invariant measurable subsets \(A \subseteq \Omega\) are null sets and the complements of null sets.

The meaning of this is clarified by ‘ergodic theorem’. Suppose \(T_t : \Omega \to \Omega\) is a measure-preserving dynamical system on a probability measure space \(\Omega,\mu\), and suppose \(f \colon \Omega \to \mathbb{R}\) is an integrable function. Then we can define two averages of \(f\), the ‘time average’ and ‘phase space average’.

Time average: This is the following average (if it exists):

$$ \widehat{f}(x) = \lim_{t\rightarrow\infty}\; \frac{1}{t} \int_0^t f(T_s x) \, ds .$$

Phase space average: This is the integral of \(f\) over the phase space:

$$ \bar{f} = \int_\Omega f \, d \mu(x). $$

In general the time average and phase space average may be difference, and the time average may not exist. But if \(T_t\) is ergodic, Birkhoff’s ergodic theorem says that

$$ \widehat{f}(x) = \bar{f} $$

for almost every \(x \in \Omega\).

Proving that a measure-preserving dynamical system is ergodic can be difficult. Bunimovich’s thesis advisor, Yakov G. Sinai, showed that a billiard moving on a square table with a reflecting disk inside is ergodic.

The curvature of the disk tends to amplify the angle between slightly different trajectories. The Bunimovich stadium is subtler because it lacks this feature: since its rounded ends are convex, they tend to focus billiards that bounce off them. The rectangular portion of the table counteracts this focusing effect, and over long enough times there tend to be an exponentially growing distance between initially nearby trajectories.

As Buminovich writes:

Moreover, a closer analysis of these billiards revealed a new mechanism of chaotic behavior of conservative dynamical systems, which is called a mechanism of defocusing. The key observation is that a narrow parallel beam of rays, after focusing because of reflection from a focusing boundary, may pass a focusing (in linear approximation) point and become divergent provided that a free path between two consecutive reflections from the boundary is long enough. The mechanism of defocusing works under condition that divergence prevails over convergence.

This is from:

• Leonid Buminovich, Dynamical billiards, Scholarpedia.

However, this analysis is not sufficient to understand the ergodicity of the Bunimovich stadium, because in 1973 Lazutkin showed that a convex billiard table with infinitely differentiable boundary cannot be ergodic. In fact he showed this for a convex table whose boundary has 553 continuous derivatives! In 1982 Douady showed 6 continuous derivatives is enough — and he conjectured that 4 is enough. For references, see:

• Nikolai Chernov and Roberto Makarian, Introduction to the Ergodic Theory of Chaotic Billiards, 2nd ed., Impa, Rio de Janeiro, 2003.

For quantum aspects of the Bunimovich stadium see:

• Terence Tao, Open question: scarring for the Bunimovich stadium, What’s New, March 28, 2007.

This explained an interesting question which was addressed by later work:

• Terence Tao, Hassell’s proof of scarring for the Bunimovich stadium, What’s New, July 7, 2008.

Also try Carlos Scheidegger’s great webpage that lets you play around with billiards on the Bunimovich stadium as well as elliptical table, where their motion is completely integrable:

• Carlos Scheidegger, Bunimovich
stadium.

Phillipe Roux put his animation of the Bunimovich stadium on Google Photos under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International license. George Stamatiou put his picture of the Sinai billiard on Wikicommons under a Creative Commons Attribution 2.5 Generic license. Jakob Scholbach put his picture of billiard trajectories in the Bunimovich stadium on Wikicommons under a Attribution-ShareAlike 3.0 Unported license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!