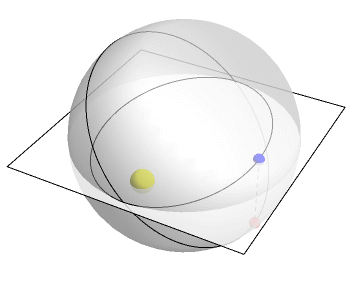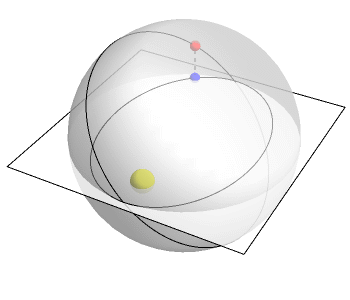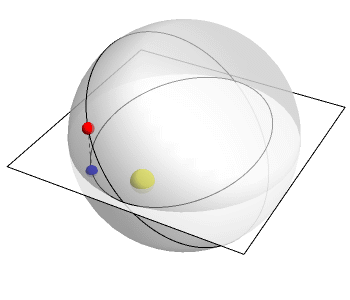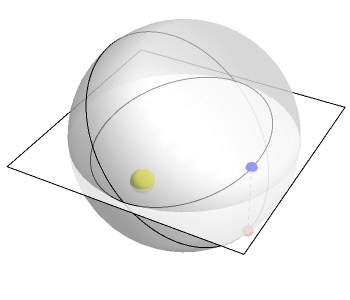
The Kepler problem concerns a particle moving under the influence of gravity, like a planet moving around the Sun. Newton showed the orbit of such a particle is an ellipse, assuming it doesn’t fly off to infinity. There are many ways to prove this, but the most illuminating is think of the orbit as a circle in 4 dimensions. When the circle is projected down to 3-dimensional space, it becomes an ellipse.

The animation above, created by Greg Egan, shows how this works. The plane represents 2 of the 3 spatial dimensions we live in. The vertical direction represents a fourth dimension. A point moves around in a circle in \(\mathbb{R}^4\). But projecting this circle down to \(\mathbb{R}^3\), we obtain an ellipse: the actual orbit of the planet.

What is the fourth dimension? It’s related to time—but it’s not exactly time. It’s the difference between ordinary time and a reparametrized version of time that flows at a rate inversely proportional to the distance between the planet and the Sun.

The animation uses this other sort of time. Relative to this other time, the planet is moving at constant speed around a circle in 4 dimensions. But in ordinary time, its projection to 3 dimensions moves faster when it’s closer to the Sun, as a planet must.

Physicists have known about this viewpoint at least since 1980, thanks to a paper by the mathematical physicist Jürgen Moser. Some parts of the story are much older. Many papers have been written about it, but this one is particularly elegant:

• Jesper Göransson, Symmetries of the Kepler problem, 8 March 2015.

The best thing about Göransson’s 4-dimensional description of planetary motion is that it gives a clean explanation of an amazing fact. You can take any elliptical orbit, apply a rotation of 4-dimensional space, and get another valid orbit!

Of course we can rotate an elliptical orbit about the sun in the usual 3-dimensional way and get another elliptical orbit. The interesting part is that we can also do 4-dimensional rotations. This can make a round ellipse look skinny: when we tilt a circle into the fourth dimension, its ‘shadow’ in 3-dimensional space becomes thinner!

In fact, you can turn any elliptical orbit into any other elliptical orbit with the same energy by a 4-dimensional rotation of this sort. All elliptical orbits with the same energy are projections of circular orbits on the same sphere in 4 dimensions!

Let us look at the mathematics in more detail.

The Kepler problem

Suppose we have a particle moving in an inverse square force law. Its equation of motion is

$$ \displaystyle{ m \ddot{\mathbf{r}} = – \frac{k \mathbf{r}}{r^3} } $$

where \( \mathbf{r}\) is its position as a function of time, \( r\) is its distance from the origin, \( m\) is its mass, and \( k\) says how strong the force is. From this we can derive the law of conservation of energy, which says

$$ \displaystyle{ \frac{m \dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} – \frac{k}{r} = E } $$

for some constant \( E\) that depends on the particle’s orbit, but doesn’t change with time.

Let’s consider an attractive force, so \( k > 0\), and elliptical orbits, so \( E < 0\). Let’s call the particle a 'planet'. It's a planet moving around the Sun, where we treat the Sun as so heavy that it remains perfectly fixed at the origin.

Let us focus attention on orbits of a single fixed energy \( E\). This frees us to choose units of mass, length and time in which

$$ m = 1, \;\; k = 1, \;\; E = -\frac{1}{2} $$

This will reduce the clutter of letters and let us focus on the key ideas. If you prefer an approach that keeps in the units, see Göransson's paper.

Now the equation of motion is

$$ \displaystyle{\ddot{\mathbf{r}} = – \frac{\mathbf{r}}{r^3} } $$

and conservation of energy says

$$ \displaystyle{ \frac{\dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} – \frac{1}{r} = -\frac{1}{2} } $$

The big idea, apparently due to Moser, is to switch from our ordinary notion of time to a new notion of time! We'll call this new time \( s\), and demand that

$$ \displaystyle{ \frac{d s}{d t} = \frac{1}{r} } $$

This new kind of time ticks more slowly as you get farther from the sun. So, using this new time speeds up the planet’s motion when it’s far from the Sun. If that seems backwards, just think about it. For a planet very far from the Sun, one day of this new time could equal a week of ordinary time. So, measured using this new time, a planet far from the sun might travel in one day what would normally take a week.

This compensates for the planet’s ordinary tendency to move slower when it’s far from the Sun. In fact, with this new kind of time, a planet moves just as fast when it’s farthest from the sun as when it’s closest.

Amazing things happens with this new notion of time! To see this, first rewrite conservation of energy using this new notion of time. We’ve been using a dot for the ordinary time derivative, following Newton. Let’s use a prime for the derivative with respect to \( s\). So, for example, we have

$$ \displaystyle{ t’ = \frac{dt}{ds} = r } $$

and

$$ \displaystyle{ \mathbf{r}’ = \frac{dr}{ds} = \frac{dt}{ds}\frac{dr}{dt} = r \dot{\mathbf{r}} } $$

Using this new kind of time derivative, Göransson shows that conservation of energy can be written as

$$ \displaystyle{ (t’ – 1)^2 + \mathbf{r}’ \cdot \mathbf{r}’ = 1 } $$

This is the equation of a sphere in 4-dimensional space!

Later we’ll see why conservation of energy can be written this way. First let’s talk about what it means. To understand it, we should treat the ordinary time coordinate \( t\) and the space coordinates \( (x,y,z)\) on an equal footing. The point

$$ (t,x,y,z) $$

moves around in 4-dimensional space as the parameter \( s\) changes. What we’re seeing is that the velocity of this point, namely

$$ \mathbf{v} = (t’,x’,y’,z’) $$

moves around on a sphere in 4-dimensional space. It’s a sphere of radius one centered at the point

$$ (1,0,0,0) $$

With some further calculation we can show some other wonderful facts:

$$ \mathbf{r}^{\prime\prime\prime} = -\mathbf{r}’ $$

and

$$ t^{\prime\prime\prime} = -(t’ – 1) $$

These are the usual equations for a harmonic oscillator, but with an extra derivative!

Proofs of these facts are below. First let’s think about what they mean. We can state both of these facts in words as follows: the 4-dimensional velocity \( \mathbf{v}\) carries out simple harmonic motion about the point \( (1,0,0,0)\).

That’s nice. But since \( \mathbf{v}\) also stays on the unit sphere centered at this point, we can conclude something even better: \( v\) must move along a great circle on this sphere, at constant speed!

This implies that the spatial components of the 4-dimensional velocity have mean \( 0\), while the \( t\) component has mean \( 1\).

The first part here makes a lot of sense: our planet doesn’t drift ever farther from the Sun, so its mean velocity must be zero. The second part is a bit subtler, but it also makes sense: the ordinary time \( t\) moves forward at speed 1 on average with respect to the new time parameter \( s\), but its rate of change oscillates in a sinusoidal way.

If we integrate both sides of

$$ \mathbf{r}^{\prime\prime\prime} = -\mathbf{r}’ $$

we obtain

$$ \mathbf{r}^{\prime\prime} = -\mathbf{r} + \mathbf{a} $$

for some constant vector \( \mathbf{a}\). This says that the position \( \mathbf{r}\) oscillates harmonically about a point \( \mathbf{a}\). Since \( \mathbf{a}\) doesn’t change with time, it’s a conserved quantity: it’s called the Runge–Lenz vector.

Often people start with the inverse square force law, show that angular momentum and the Runge–Lenz vector are conserved, and use these 6 conserved quantities and Noether’s theorem to show there’s a 6-dimensional group of symmetries. For solutions with negative energy, this turns out to be the group of rotations in 4 dimensions, \( \mathrm{SO}(4)\). With more work, we can see how the Kepler problem is related to a harmonic oscillator in 4 dimensions. Doing this involves reparametrizing time.

I like Göransson’s approach better in many ways, because it starts by biting the bullet and reparametrizing time. This lets him rather efficiently show that the planet’s elliptical orbit is a projection to 3-dimensional space of a circular orbit in 4d space. The 4d rotational symmetry is then evident!

Göransson actually carries out his argument for an inverse square law in \(n\)-dimensional space; it’s no harder. The elliptical orbits in \(n\) dimensions are projections of circular orbits in \(n+1\) dimensions. Angular momentum is a bivector in \(n\) dimensions; together with the Runge–Lenz vector it forms a bivector in \(n+1\) dimensions. This is the conserved quantity associated to the \((n+1)\)-dimensional rotational symmetry of the problem.

He also carries out the analogous argument for positive-energy orbits, which are hyperbolas, and zero-energy orbits, which are parabolas. The hyperbolic case has the Lorentz group symmetry and the zero-energy case has Euclidean group symmetry! This was already known, but it’s nice to see how easily Göransson’s calculations handle all three cases.

Mathematical details

Checking all this is a straightforward exercise in vector calculus, but it takes a bit of work, so let me do some here. There will still be details left to fill in, and I urge that you give it a try.

Remember, our reparametrization of time gives

$$ t’ = r , \qquad \mathbf{r}’ = r \dot{\mathbf{r}} $$

where the prime stands for \(d/ds\). Thus, we can start with conservation of energy:

$$ \displaystyle{ \frac{\dot{\mathbf{r}} \cdot \dot{\mathbf{r}}}{2} – \frac{1}{r} = -\frac{1}{2} } $$

and use

$$ \displaystyle{ \dot{\mathbf{r}} = \frac{d\mathbf{r}/dt}{dt/ds} = \frac{\mathbf{r}’}{t’} } $$

to obtain

$$ \displaystyle{ \frac{\mathbf{r}’ \cdot \mathbf{r}’}{2 t’^2} – \frac{1}{t’} = -\frac{1}{2} } $$

With a little algebra this gives

$$ \displaystyle{ \mathbf{r}’ \cdot \mathbf{r}’ + (t’ – 1)^2 = 1} $$

This shows that the 4-velocity

$$ \mathbf{v} = (t’,x’,y’,z’) $$

stays on the unit sphere centered at \( (1,0,0,0)\).

The next step is to take the equation of motion

$$ \displaystyle{\ddot{\mathbf{r}} = – \frac{\mathbf{r}}{r^3} } $$

and rewrite it using primes (\( s\) derivatives) instead of dots (\( t\) derivatives). We start with

$$ \displaystyle{ \dot{\mathbf{r}} = \frac{\mathbf{r}’}{r} } $$

and differentiate again to get

$$ \ddot{\mathbf{r}} = \displaystyle{ \frac{1}{r} \left(\frac{\mathbf{r}’}{r}\right)’ } = \displaystyle{ \frac{1}{r} \left( \frac{r \mathbf{r}^{\prime\prime} – r’ \mathbf{r}’}{r^2} \right) } = \displaystyle{ \frac{r \mathbf{r}^{\prime\prime} – r’ \mathbf{r}’}{r^3} } $$

Next, our other equation for \( \ddot{\mathbf{r}}\) gives

$$ \displaystyle{ \frac{r \mathbf{r}^{\prime\prime} – r’ \mathbf{r}’}{r^3} = – \frac{\mathbf{r}}{r^3} } $$

or

$$ r \mathbf{r}^{\prime\prime} – r’ \mathbf{r}’ = -\mathbf{r} $$

so

$$ \displaystyle{ \mathbf{r}^{\prime\prime} = \frac{r’ \mathbf{r}’ – \mathbf{r}}{r} } $$

To go further, it’s good to get a formula for \( r^{\prime\prime}\) as well. First we compute

$$ r’ = \displaystyle{ \frac{d}{ds} (\mathbf{r} \cdot \mathbf{r})^{\frac{1}{2}} } = \displaystyle{ \frac{\mathbf{r}’ \cdot \mathbf{r}}{r} } $$

and then differentiating again,

$$ r^{\prime\prime} = \displaystyle{\frac{d}{ds} \frac{\mathbf{r}’ \cdot \mathbf{r}}{r} } = \displaystyle{ \frac{r \mathbf{r}^{\prime\prime} \cdot \mathbf{r} + r \mathbf{r}’ \cdot \mathbf{r}’ – r’ \mathbf{r}’ \cdot \mathbf{r}}{r^2} } $$

Plugging in the formula for \( \mathbf{r}^{\prime\prime}\), some wonderful cancellations occur and we obtain

$$ r^{\prime\prime} = \displaystyle{ \frac{\mathbf{r}’ \cdot \mathbf{r}’}{r} – 1 } $$

But we can do better! Remember, conservation of energy says

$$ \displaystyle{ \mathbf{r}’ \cdot \mathbf{r}’ + (t’ – 1)^2 = 1} $$

and we know \( t’ = r\). So,

$$ \mathbf{r}’ \cdot \mathbf{r}’ = 1 – (r – 1)^2 = 2r – r^2 $$

and

$$ r^{\prime\prime} = \displaystyle{ \frac{\mathbf{r}’ \cdot \mathbf{r}’}{r} – 1 } = 1 – r $$

So, we see

$$ r^{\prime\prime} = 1 – r $$

Since \(t’ = r\) this gives

$$ t^{\prime\prime\prime} = 1 – t’ $$

as desired.

Next let’s get a similar formula for \( \mathbf{r}^{\prime\prime\prime}\). We start with

$$ \displaystyle{ \mathbf{r}^{\prime\prime} = \frac{r’ \mathbf{r}’ – \mathbf{r}}{r} } $$

and differentiate both sides to get

$$ \displaystyle{ \mathbf{r}^{\prime\prime\prime} = \frac{r r^{\prime\prime} \mathbf{r}’ + r r’ \mathbf{r}^{\prime\prime} – r \mathbf{r}’ – r’}{r^2} } $$

Then plug in our formulas for \( r^{\prime\prime} \) and \( \mathbf{r}^{\prime\prime} \). Some truly miraculous cancellations occur and we obtain

$$ \mathbf{r}^{\prime\prime\prime} = -\mathbf{r}’ $$

as desired.

Integrating both sides of this, we then get

$$ \mathbf{r}^{\prime\prime} = -\mathbf{r} + \mathbf{a} $$

for some fixed vector \( \mathbf{a}\), the Runge–Lenz vector. This says \( \mathbf{r}\) undergoes harmonic motion about \( \mathbf{a}\). It’s quite remarkable that both \( \mathbf{r}\) and its norm \( r\) undergo harmonic motion!

The quantum version of a planetary orbit is a hydrogen atom, and everything we have just seen has a quantum analogue. For more on that, see:

• Greg Egan, The ellipse and the atom.

For more of the history of this problem, see:

• John Baez, Mysteries of the gravitational 2-body problem.

This also treats quantum aspects, connections to supersymmetry and Jordan algebras, and more.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!