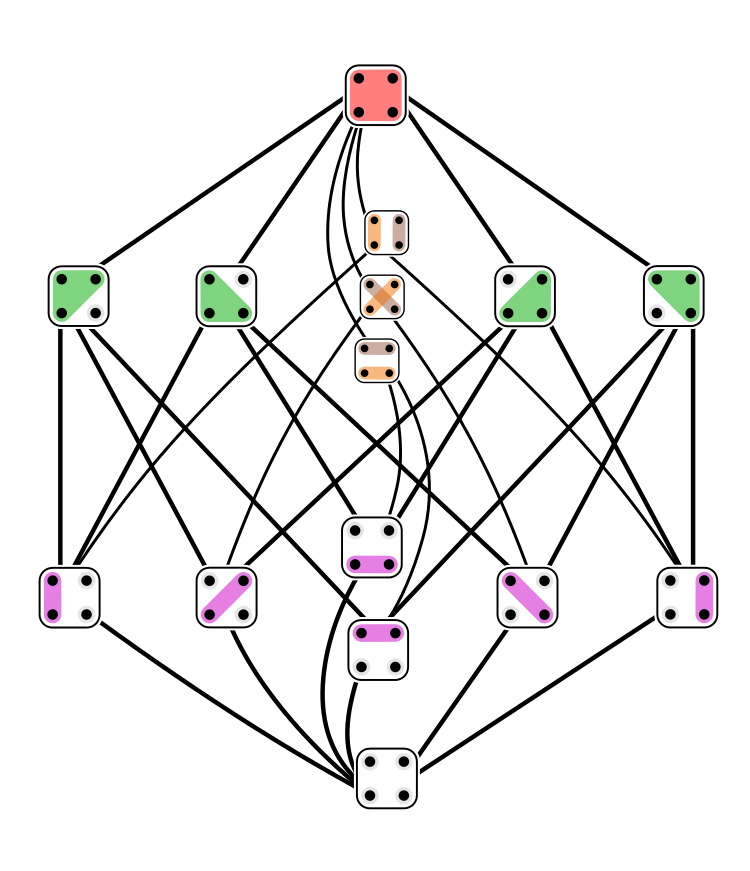
This picture by Tilman Piesk shows the 15 partitions of a 4-element set, ordered by refinement. Coarser partitions are connected to finer ones by lines going down. In the ‘coarsest’ partition, on top, all 4 elements are in the same subset. In the ‘finest’ one, on bottom, each of the 4 elements is in its own subset.

A partition of a set $S$ is a way of writing it as a disjoint union of nonempty subsets called blocks. There is a natural 1-1 correspondence between partitions $S$ and equivalence relations on $S$, so the two concepts are just different ways of thinking about the same thing.

We say the equivalence relation $\sim$ is finer than the equivalence relation $\sim’$ if

$$ x \sim y \; \implies x \sim’ y $$

In this situation we also say that $\sim’$ is coarser than $\sim$. We also use these words for the partitions corresponding to these equivalence relations. A partition $\pi$ is finer than a partition $\pi’$ iff every block of $\pi$ is contained in a block of $\pi’$.

This puts a partial ordering on the set $\Pi(S)$ of all partitions of $S$: we say $\pi \le \pi’$ if $\pi$ is finer than $\pi’$. In fact this makes $\Pi(S)$ into a complete lattice. This lattice is much subtler than the lattice of subsets of $S$: for example, it typically fails to be distributive.

Puzzle 1: Can you see how the lattice here fails to be distributive? If $p \vee q$ is the coarsest partition finer than both $p$ and $q$, and $p \wedge q$ is the finest partition that is coarser than both $p$ and $q$, you want to find partitions with

$$ p \wedge (q \vee r) \ne (p \wedge q) \vee (p \wedge r) $$

or

$$ p \vee (q \wedge r) \ne (p \vee q) \wedge (p \vee r) $$

The lattice of partitions $\Pi(S)$ also typically lacks the Sperner property. In other words, the largest possible set of partitions of $S$, none of which is finer than any other, does not consist of all partitions with a specific number of blocks. However, the first proof of this, due to E. R. Canfield, only constructed counterexamples when $S$ has more than about $6.5 \cdot 10^{24}$ elements! The challenge of understanding these counterexamples in full detail has a fascinating history, some of which is told here:

• E. Rodney Canfield, On a problem of Rota, Adv. Math. 29 (1978), 1–10.

• Ronald Graham, Maximum antichains in the partition lattice, The Mathematical Intelligencer 2 (1978), 84–86.

• E. Rodney Canfield and Larry H. Harper, A simplified guide to large antichains in the partition lattice, December 13, 1999.

Counting the number of partitions of an $n$-element set gives the $n$th Bell number $B_n$. The Bell numbers have a nice generating function:

$$ \displaystyle{ \sum_{n = 0}^\infty \frac{B_n z^n}{n!} = e^{e^z – 1} }$$

and Dobinski’s formula is quite charming:

$$ B_n = \displaystyle{ \frac{1}{e} \sum_{k = 0}^\infty \frac{k^n}{k!} }.$$

but to efficiently compute the Bell numbers, it is more practical to use this easily proved recurrence relation:

$$ \displaystyle{ B_{n+1}= \sum_{k=0}^{n} \binom{n}{k} B_k .} $$

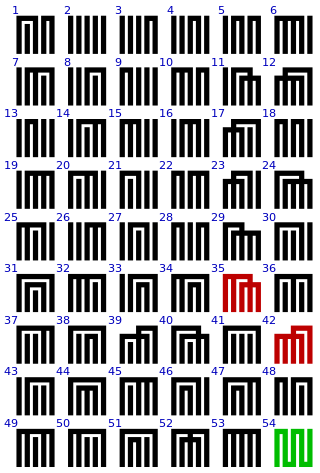
The Tale of Genji is a wonderful early Japanese novel written by the noblewoman Murasaki Shikibu sometime between 1008 and 1021 AD. It has 54 chapters. Above you see the 54 Genji-mon: the traditional symbols for these chapters. Most of them follow a systematic mathematical pattern, but the ones in color break this pattern.

Puzzle 2: How is the green Genji-mon different from all the rest?

Puzzle 3: How are the red Genji-mon similar to each other?

Puzzle 4: How are the red Genji-mon different from all the rest?

Puzzle 5: If The Tale of Genji had just 52 chapters, the Genji-mon could be perfectly systematic, without the strange features exhibited by those shown in color. What would the pattern be then?

The lattice of partitions was drawn by Tilman Piesk and placed on Wikicommons under a Creative Commons Attribution 3.0 Unported license. The chart of Genji-mon was created by ‘AnonMoos’ and put into the public domain on Wikicommons.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!