Balaban 11-Cage

/ 1 November, 2015
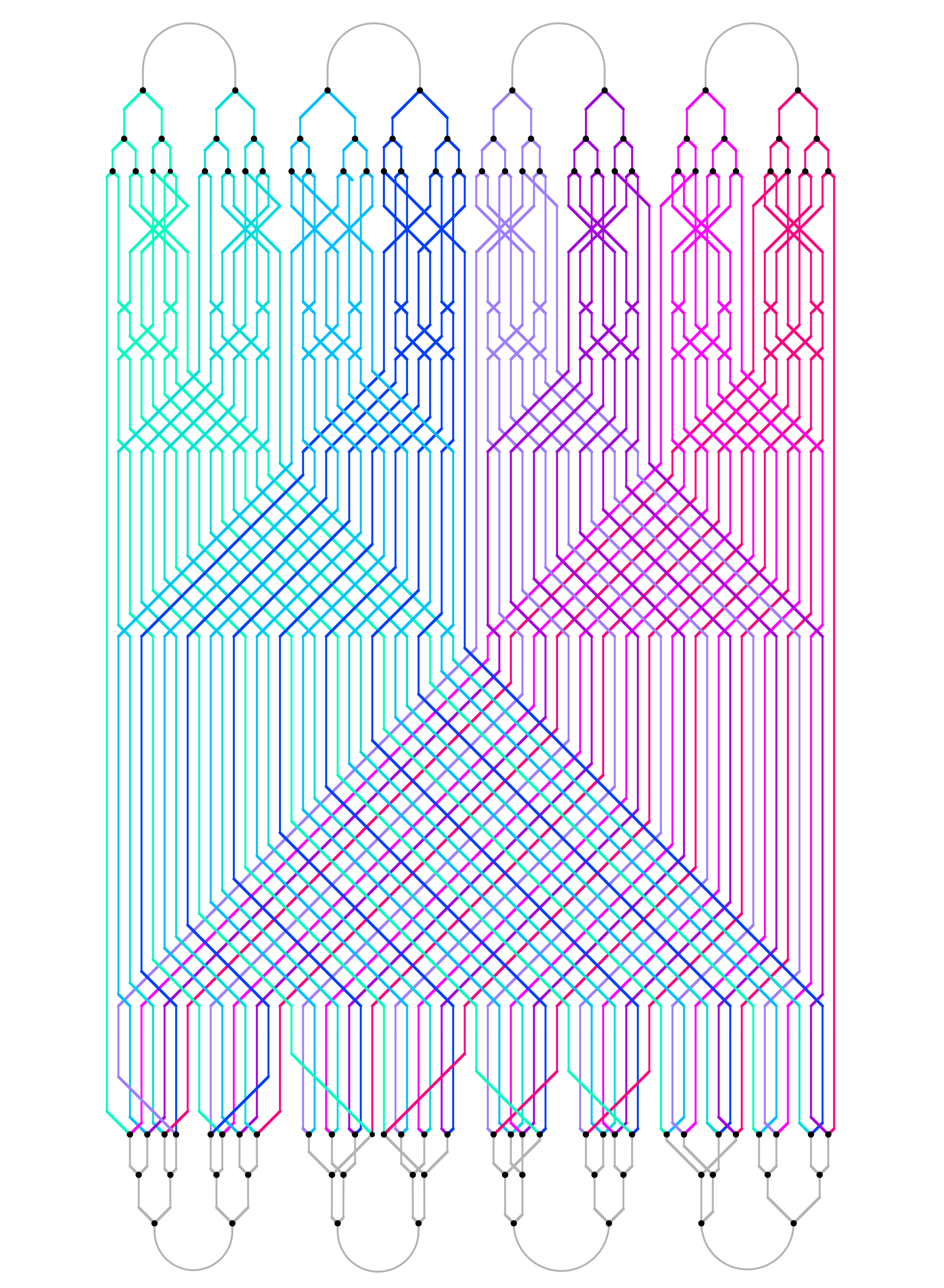
Balaban 11-Cage - Félix de la Fuente

Balaban 11-Cage – Félix de la Fuente

Félix de la Fuente is an architect and dedicated amateur mathematician in love with discrete geometry, polytopes and combinatorics. This picture created by him shows a graph called the Balaban 11-cage.

A (3,11)-graph is a simple graph where every vertex has 3 neighbors and the shortest cycle has length 11. A (3,11)-cage is a (3,11)-graph with the least possible number of vertices. The Balaban 11-cage is the unique (3,11)-cage.

The Balaban 11-cage has 112 vertices and 168 edges. It was discovered by Balaban in 1973, and its uniqueness was proved by McKay and Myrvold in 2003.

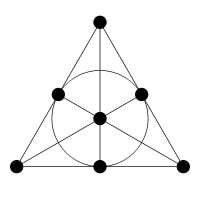
Fano Plane - Gunther

Fano Plane

Puzzle: The Fano plane has 168 symmetries, and it contains 28 triangles and also 28 ways of selecting a point and a line that are not incident to each other. 112 is 4 times 28. Is there a way to build the Balaban 11-cage starting from the Fano plane? One obstacle is that the Balaban 11-cage has a symmetry group of order 64.

The layout for this picture comes from here:

• P. Eades, J. Marks, P. Mutzel and S. North, Graph-drawing contest report, TR98-16, Mitsubishi Electric Research Laboratories, December 1998.

A German Wikicommons user named Gunther drew the picture of the Fano plane, put it on Wikicommons, and released it into the public domain.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

Related posts

3 thoughts on “Balaban 11-Cage”

  1. Unfortunately there are errors in the picture I originally posted, which can be found on Wikimedia commons. The problems were noted by Viktor Toth:

    When I look at the top of the diagram, I see (going from top to bottom): 8×3 vertices with three neighbors each; next, 8×4 vertices with three neighbors each; and next, 8×8 verticies with TWO neighbors each.

    If I ignore the 8×8 two-neighbor vertices, I am left with 56 vertices; another 56 are at the bottom brings the total to 112, which is exactly the number of vertices Balaban’s 11-cage supposedly has.

    So from this I have to conclude that the 8×8 two-neighbor vertices at the top (and their counterparts at the bottom), 128 vertices in total, are purely decorative and are not to be seen as actual vertices.

    and then:

    I looked at the SVG and it could be edited, though it’s a bit of a chore, as editing requires not only removing the unwanted vertices but also lengthening some edges. However, I found other problems with the diagram: the 37th and 45th vertices in the bottom continuous row are orphans, so obviously some edges are misplaced there. So there is a good chance that even after the unwanted vertices are removed, the resulting diagram will still be erroneous. It might be a better idea to re-generate a proper diagram algorithmically.

    Luckily Félix de la Fuente drew a better picture!

  2. “The Balaban 11-cage has 112 edges and 168 edges.”

    I think there’s an inconsistency in that line.

Comments are closed.