Gravity Plus Inverse Cube Force – WillowW

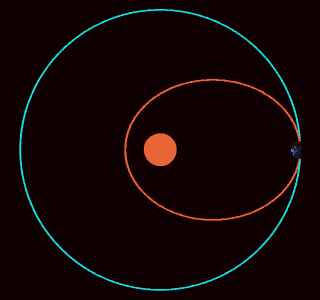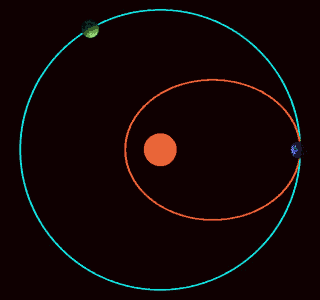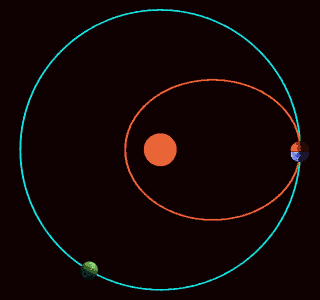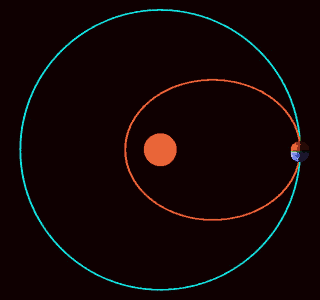
This image shows three imaginary planets orbiting the Sun. The blue planet follows a realistic trajectory: under the influence of an inverse-square force, it orbits in an ellipse. The green and red planets have the same radial motion as the blue one, so they stay on the same circle, which expands and contracts. However, these planets moves around the Sun more slowly. The green planet makes just 1 revolution for each 3 of the blue one, and the red one doesn’t move around at all!

What could make a planet move like in these strange ways? Newton figured this out in his Principia Mathematica. In Propositions 43–45 of Book I, he showed that an inverse cube force law will do the job.

Recall that a central force is one that only pushes a particle towards or away from some chosen point, and only depends on the particle’s distance from that point. In Newton’s theory, gravity is a central force obeying an inverse square law:

$$ F(r) = \;- \displaystyle{ \frac{a}{r^2} } $$

for some constant \(a.\) But he considered adding an extra central force obeying an inverse cube law:

$$ F(r) = \; – \displaystyle{ \frac{a}{r^2} + \frac{b}{r^3} } $$

He showed that if you do this, for any motion of a particle in the force of gravity you can find a motion of a particle in gravity plus this extra force, where the distance \(r(t)\) is the same, but the angle \(\theta(t)\) is not.

In fact, he showed that if we start with any central force, adding an inverse cube force has this effect. This is his apsidal precession theorem.

It’s easy to see this result using more modern ideas. A particle in a central force will move in a plane, so we can use polar coordinates \(r, \theta\) to describe its position. We can describe the force away from the origin as a function \(F(r).\) The radial part of the particle’s motion obeys this equation:

$$ \displaystyle{ m \ddot r = F(r) + \frac{L^2}{mr^3} } $$

where \(L\) is the particle’s angular momentum and \(m\) is its mass. So, if we add an inverse cube term to the force \(F(r)\), while changing \(L\) in a way that exactly compensates, the equation for \(m \ddot{r}\) does not change. Thus, the radial motion of the particle will be unchanged. However, changing the angular momentum changes the particle’s angular motion, since

$$ m r^2 \dot{\theta} = L .$$

For more see:

• Newton’s theorem of revolving orbits, Wikipedia.

• S. R. Valluri, C. Wilson and W. Harper, Newton’s apsidal precession theorem and eccentric orbits, Journal for the History of Astronomy 95 (1997), 13–27.

This animated gif was made by ‘WillowW’ and placed on Wikicommons under a Creative Commons Attribution 3.0 Unported license. It was then compressed to a size suitable for this blog by Marco Devillers.