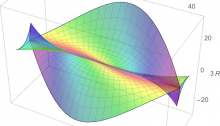
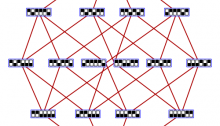
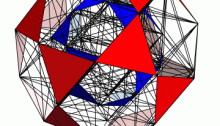
Discriminant of the Icosahedral Group

This image, created by Greg Egan, shows the ‘discriminant’ of the symmetry group of the icosahedron. This group acts as linear transformations of $\mathbb{R}^3$ and thus also $\mathbb{C}^3$ . By a theorem of Chevalley, the space of orbits of this group action is again isomorphic to $\mathbb{C}^3$ . Each point in the surface shown here corresponds to a ‘nongeneric’ orbit: an orbit with fewer than the maximal number of points. More precisely, the space of nongeneric orbits forms a complex surface in $\mathbb{C}^3$ , called the discriminant, whose intersection with $\mathbb{R}^3$ is shown here.

Hoffman–Singleton Graph

This is the Hoffman–Singleton graph, a remarkably symmetrical graph with 50 vertices and 175 edges. There is a beautiful way to construct the Hoffman–Singleton graph by connecting 5 pentagons to 5 pentagrams.

Free Modular Lattice on 3 Generators

This is the free modular lattice on 3 generators, as drawn by Jesse McKeown. First discovered by Dedekind in 1900, this structure turns out to have an interesting connection to 8-dimensional Euclidean space.

Golay Code

The extended binary Golay code, or Golay code for short, is a way to encode 12 bits of data in a 24-bit word in such a way that any 3-bit error can be corrected, and any 7-bit error can at least be detected. The easiest way to understand this code uses the geometry of the dodecahedron, as shown in this image by Gerard Westendorp.

McGee Graph

This is the McGee graph. It is 3-regular graph, meaning that every vertex has 3 neighbors. It also has girth 7, meaning that the shortest cycles have length 7. What makes the McGee graph special is that it has the least number of vertices of any 3-regular graph of girth 7.

Hypercube of Duads

This picture by Greg Egan shows a hypercube with all vertices except the bottom labelled by duads, that is, 2-element subsets of a 6-element set. There are 15 duads, while the hypercube has 16 vertices.

Tutte–Coxeter Graph

This picture shows the Tutte–Coxeter graph. This graph was discovered by the famous graph theorist William Thomas Tutte in 1947, but its remarkable properties were studied further by him and the geometer H. S. M. Coxeter in a pair of papers published in 1958.

Heawood Graph

This is the Heawood graph. This graph can be drawn on a torus with no edges crossing in such a way that it divides the torus into 7 hexagons, each pair of which shares an edge. In 1890, Percy John Heawood proved that for any map drawn on a torus, it takes at most 7 colors to ensure that no two countries sharing a common boundary have the same color. The Heawood graph proves that the number 7 is optimal.

Icosidodecahedron from Projected D6 Root Polytope - Greg Egan

Icosidodecahedron from D6

The icosidodecahedron can be built by truncating either an icosahedron or a dodecahedron. It has 30 vertices. It is a beautiful, highly symmetrical shape. But it’s just a shadow of an even more symmetrical shape with twice as many vertices in twice as many dimensions!

2-adic Integers

This image created by Christopher Culter shows the compact abelian group of 2-adic integers (black points), with selected elements labeled by the corresponding character on the Pontryagin dual group (colored discs).

Visual Insight

Mathematics Made Visible

Groups

Discriminant of the Icosahedral Group

Hoffman–Singleton Graph

Free Modular Lattice on 3 Generators

Golay Code

McGee Graph

Hypercube of Duads

Tutte–Coxeter Graph

Heawood Graph

Icosidodecahedron from D6

2-adic Integers

Publications

Membership

Meetings & Conferences

News & Public Outreach

The Profession

Programs

Government Relations

About the AMS