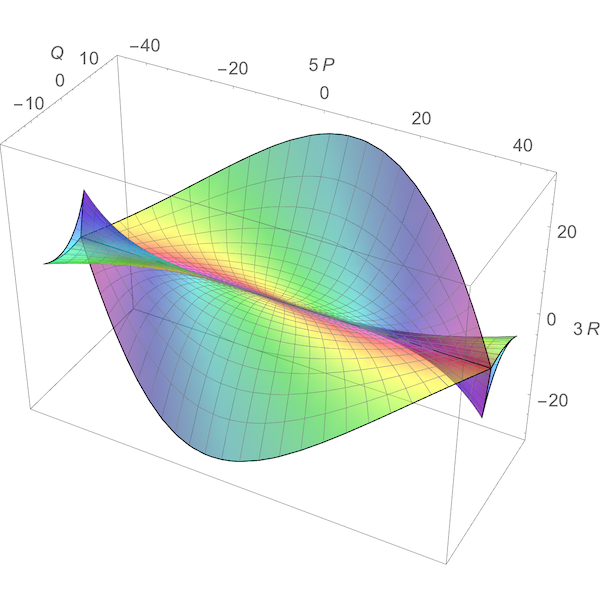
This image, created by Greg Egan, shows the ‘discriminant’ of the symmetry group of the icosahedron. This group acts as linear transformations of \(\mathbb{R}^3\) and thus also \(\mathbb{C}^3\). By a theorem of Chevalley, the space of orbits of this group action is again isomorphic to \(\mathbb{C}^3\). Each point in the surface shown here corresponds to a ‘nongeneric’ orbit: an orbit with fewer than the maximal number of points. More precisely, the space of nongeneric orbits forms a complex surface in \(\mathbb{C}^3\), called the discriminant, whose intersection with \(\mathbb{R}^3\) is shown here.

The symmetry group of the icosahedron, also known as \(\textrm{H}_3\), has 120 elements. We can think of it as the group of linear transformations of \(\mathbb{R}^3\) preserving a set of planes called mirrors. In fact \(\textrm{H}_3\) is generated by reflections through these mirrors.

If we intersect these mirrors with the unit sphere we get the Coxeter complex for \(\textrm{H}_3\), which looks like this:

There are 120 spherical triangles in this picture. The group \(\textrm{H}_3\) acts freely and transitively on these, with reflections switching the black and blue triangles. Any point in the interior of one of these triangles is said to lie in a generic orbit of \(\textrm{H}_3\), an orbit containing 120 elements. Points on the edges and vertices lie in nongeneric orbits: that is, orbits with fewer than 120 elements.

There is a unique way to extend the action of \(\textrm{H}_3\) as real-linear transformations of \(\mathbb{R}^3\) to an action as complex-linear transformations of \(\mathbb{C}^3\). By a theorem of Chevalley, the space of orbits of this group action on \(\mathbb{C}^3\) is again isomorphic to \(\mathbb{C}^3\). Inside this copy of \(\mathbb{C}^3\) there is a complex surface consisting of the nongeneric orbits. This is called the discriminant of \(\textrm{H}_3\). Egan’s picture shows the intersection of this discriminant with \(\mathbb{R}^3\).

How did Egan create this picture? For that we need to understand a bit of the proof of Chevalley’s theorem, to get an explicit map giving the isomorphism between the space of \(\textrm{H}_3\) orbits in \( \mathbb{C}^3\) and \(\mathbb{C}^3\) itself.

Certain polynomials in \(x,y,z\) are invariant when we apply any of the icosahedron symmetries. Apart from constants, the most obvious has degree 2:

$$ P(x,y,z) = x^2 + y^2 + z^2 $$

There is also an invariant polynomial of degree 6 that we obtain as follows. The icosahedron has 12 vertices, which come in opposite pairs. Choose 6 vertices \(q_1, \dots, q_6,\) none opposite to each other. Taking the dot product with each of these gives a linear function:

$$ f_i(x,y,z) = q_i \cdot (x,y,z) $$

Multiplying all 6 of these linear functions gives an an invariant polynomial:

$$ Q(x,y,z) = f_1(x,y,z) \cdots f_6(x,y,z) $$

There is also an invariant polynomial of degree 10 that we get as follows. The icosahedron has 20 faces, which come in opposite pairs. Choose the midpoints \(r_1, \dots, r_{10}\) of 10 faces, none opposite to each other. Taking the dot product with each of these gives a linear function:

$$ g_i(x,y,z) = r_i \cdot (x,y,z) $$

Multiplying all 10 of these linear functions gives an invariant polynomial:

$$ R(x,y,z) = g_1(x,y,z) \cdots g_{10}(x,y,z) $$

It is not instantly obvious that \(Q\) and \(R\) are invariant. Because we arbitrarily chose one corner from each opposite pair, and similarly one face from each opposite pair, \(Q\) and \(R\) could in theory change sign when we apply a symmetry of the icosahedron.

Puzzle 1. Why don’t they change sign?

Since \(P,Q,R\) are invariant under the action of \(\mathrm{H}_3\), the map

$$ \begin{array}{cccl} f : & \mathbb{C}^3 & \to & \mathbb{C}^3 \\
& (x,y,z)& \mapsto &(P(x,y,z), Q(x,y,z), R(x,y,z)) \end{array} $$

is also invariant. Egan’s picture shows the image of all the nongeneric orbits under this map.

Since \(f\) is invariant under the action of \(\mathrm{H}_3\), it factors through a map

$$ g : \mathbb{C}^3 / \mathrm{H}_3 \to \mathbb{C}^3 $$

Chevalley proved that every polynomial in \(x,y,z\) that is invariant under the action of \(\mathrm{H}_3\) can be expressed as a polynomial in \(P,Q\), and \(R\). Even better, it can be expressed as such a polynomial in a unique way. In other words, \(P,Q,R\) do not obey any nontrivial algebraic relations like \(P^2 Q = R\). These two facts are crucial to proving that \(g\) is an isomorphism of algebraic varieties.

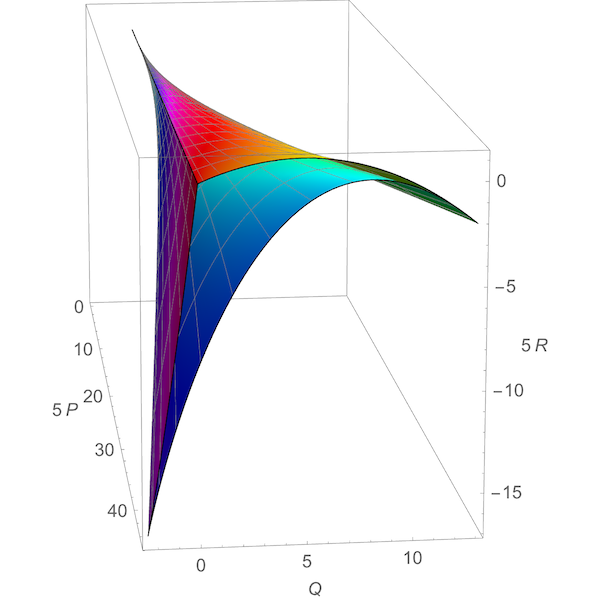
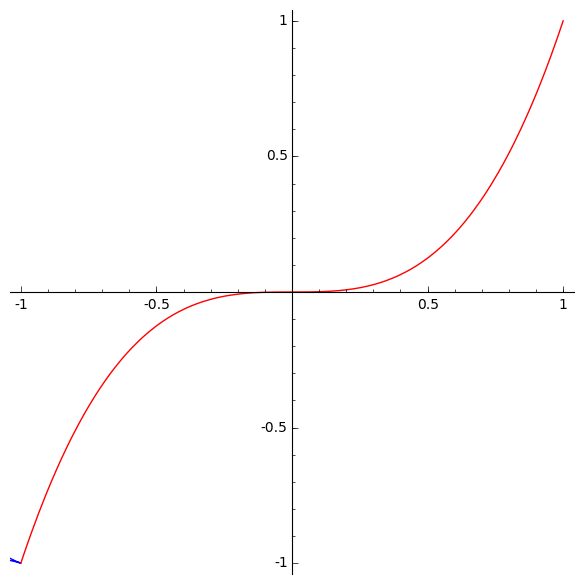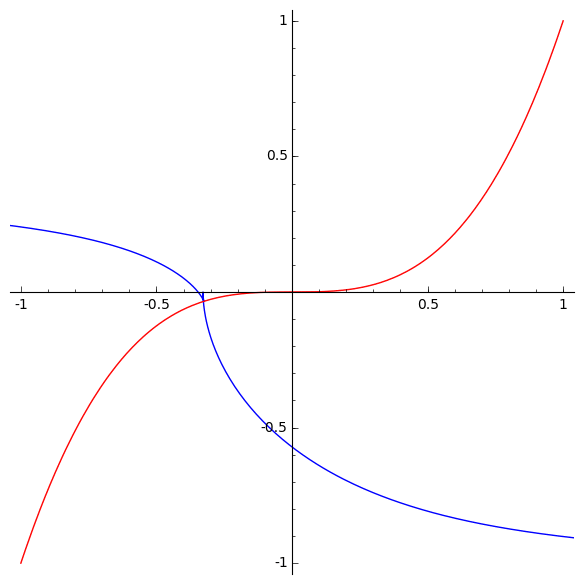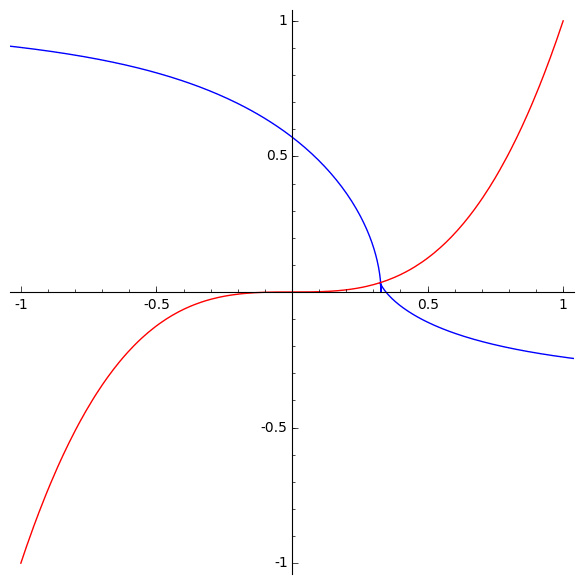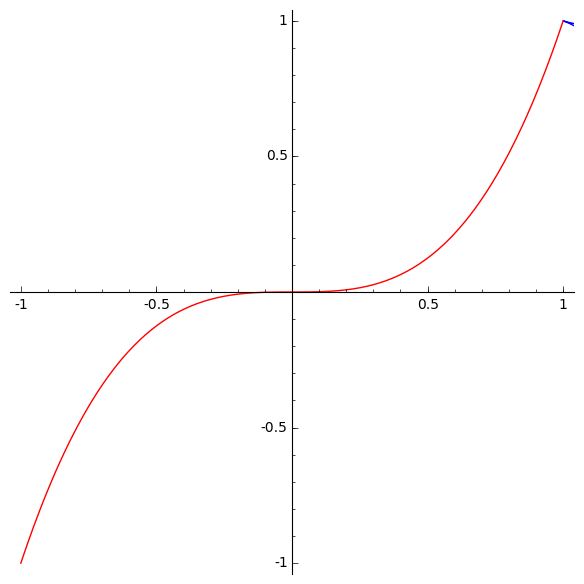
The mirrors are 2-dimensional real subspaces of \(\mathbb{R}^3\). The image of any mirror under \(g\) is just a portion of the discriminant, namely this surface in \(\mathbb{R}^3\):

This surface has two lines of cusps, one of order 3/2 near the bottom of the picture and one of order 5/2 at right. If we complexify a mirror and then take its image under \(g\), we get a larger set, namely the whole discriminant. This is shown in \(P,Q,R\) space here:

Relation to the involutes of a cubical parabola

The cusps of orders 3/2 and 5/2 should remind us of this previous post:

• Involutes of a cubical parabola.

There we discussed a one-parameter family of curves that look like slices of the discriminant of \(\mathrm{H}_3\). Here they are:

So, there is a fascinating and mysterious relationship between the discriminant of \(\mathrm{H}_3\) and the involutes of the cubical parabola!

V. I. Arnol’d discussed this in his book The Theory of Singularities and its Applications:

The discriminant of the group \(\mathrm{H}_3\) is shown in Fig. 18. Its singularities were studied by O. V. Lyashko (1982) with the help of a computer. This surface has two smooth cusped edges, one of order 3/2 and the other of order 5/2. Both are cubically tangent at the origin. Lyashko has also proved that this surface is diffeomorphic to the set of polynomials \(x^5 + ax^4 + bx^2 + c\) having a multiple root.

The comparison of this discriminant with the patterns of the propagation of the perturbations on a manifold with boundary (studied as early as in the textbook of L’Hopital in the form of the theory of evolutes of plane curves), has led A. B. Givental to the conjecture (later proven by O. P. Shcherbak) that this discriminant it locally diffeomorphic to the graph of the multivalued time function in the plane problem on the shortest path, on a manifold with boundary, which is a generic plane curve.

Thus the propagation of the waves, on a 2-manifold with boundary, is controlled by an icosahedron hidden at the inflection point of the boundary. This icosahedron is hidden, and it is difficult to find it even if its existence is known.

He then goes on to claim that the discriminant of \(\mathrm{H}_3\) is diffeomorphic to a surface built from the involutes of the cubical parabola. Unfortunately there seems to be no proof in the literature.

Puzzle 2. Can you find a proof of this fact, or give your own proof?

On page 169 of his paper ‘Singularities of systems of rays’, Arnol’d includes a hand-drawn figure similar to Egan’s picture featured in this post. He writes:

Fig. 31 illustrates the reamer of the monomial curve (1, 3, 5). Lyashko has proved that this is a surface with two edges of regression (one of type 3/2 and the other of type 5/2) tangent to each other cubically and diffeomorphic to the variety of irregular orbits of the Coxeter group \(\mathrm{H}_3\) (that is, the group of symmetries of the icosahedron). Shcherbak has proved that the reamers of all the curves \(x = t,\) \(y = t^3+ \dots ,\) \(z = t^5 \dots\) are locally diffeomorphic to the same surface. From this there follows, amongst other things, a proof of the conjecture of Givental that the graph I drew of the many-valued function of time in the problem of going around an obstacle bounded by a plane curve with a cubic point of inflection is in the neighbourhood of this point diffeomorphic to the variety of irregular orbits of the group of symmetries of the icosahedron, drawn by Lyashko. This is because this graph, as is easy to see, is the reamer of a curve of the form described above.

Unfortunately, I have not been able to find the details of Shcherbak’s proof, though he discussed related issues in a couple of papers listed below.

References

Chevalley’s result is here:

• C. Chevalley, Invariants of finite groups generated by reflections, Amer. J. Math. 77 (1955), 778–782.

Related results were proved by Coxeter and Todd.

For more details concerning the discriminant of the icosahedral group, see pages 28–31 of this book:

• Vladimir I. Arnol’d, The Theory of Singularities and its Applications, Cambridge U. Press, Cambridge, 1991.

Also see page 169 in the English version of the following paper, or page 143 in the original Russian version, which is open-access:

• Vladimir I. Arnol’d, Singularities of systems of rays, Uspekhi Mat. Nauk 38:2 (1983), 77–147. English translation in Russian Math. Surveys 38:2 (1983), 77–176.

Also see section III of this paper, which contains explicit formulas for the discriminant of the icosahedral group:

• O. Y. Lyashko, Classification of critical points of functions on a manifold with singular boundary, Funktsional. Anal. i Prilozhen. 17:3 (1983), 28–36. English translation in Functional Analysis and Its Applications 17:3 (1983), 187–193

Shcherbak’s papers also give useful hints toward a solution of Puzzle 2. Perhaps an expert could construct a full proof based on these hints:

• O. P. Shcherbak, Singularities of a family of evolvents in the neighbourhood of a point of inflection of a curve, and the group \( \mathrm{H}_3\) generated by reflections, Funktsional. Anal. i Prilozhen. 17:4 (1983), 70–72. English translation in Functional Anal. Appl. 17:4 (1983), 301–303.

• O. P. Shcherbak, Wavefronts and reflection groups, Uspekhi Mat. Nauk 43:3 (1988), 125–160. English translation in Russian Mathematical Surveys 43:3 (1988), 1497–194.

All these sources discuss the discoveries of Arnol’d and his colleagues relating singularities and Coxeter–Dynkin diagrams, starting with the more familiar \(\mathrm{ADE}\) cases, then moving on to the non-simply-laced cases, and finally the non-crystallographic cases related to \(\mathrm{H}_2\) (the symmetry group of the pentagon), \(\mathrm{H}_3\) (the symmetry group of the icosahedron) and \(\mathrm{H}_4\) (the symmetry group of the 600-cell).

The picture of the Coxeter complex for \(\mathrm{H}_3\) was created by Tom Ruen using Jeff Weeks’ Kaleidotile program and placed into the public domain on Wikicommons.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!