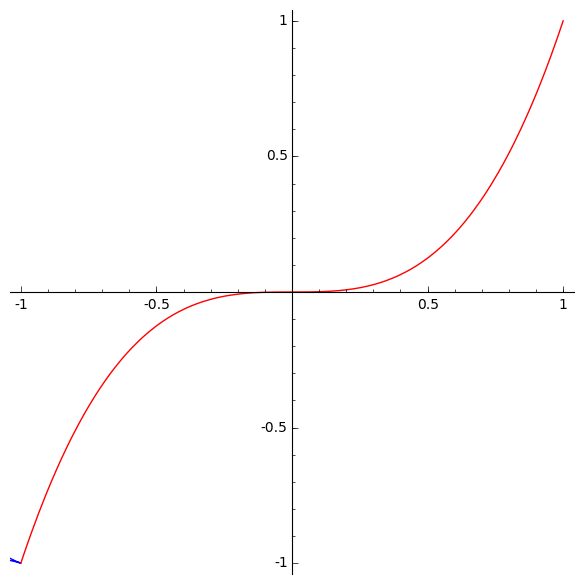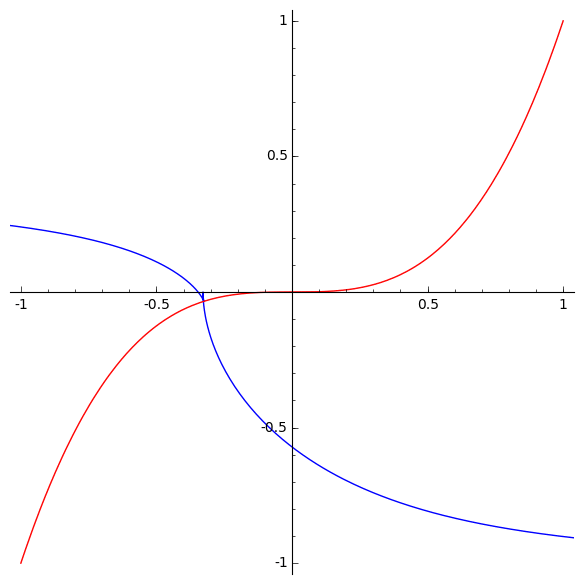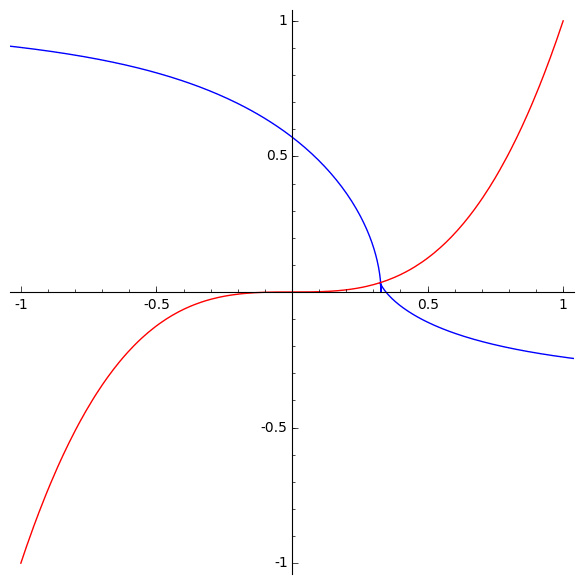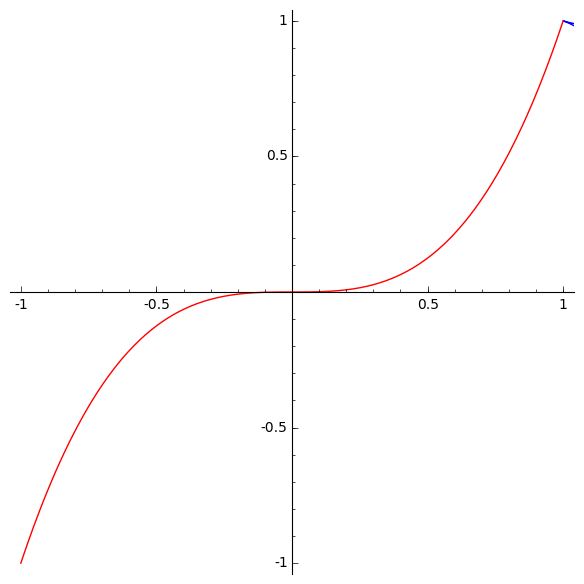
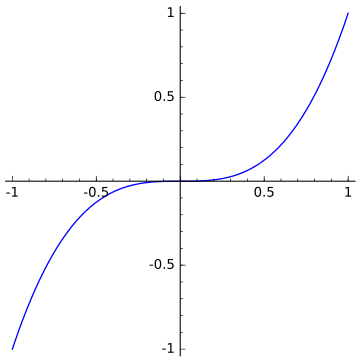
This animation by Marshall Hampton shows the involutes of the curve \(y = x^3\). It lies at a fascinating mathematical crossroads, which we shall explore in a series of three posts, namely the current post and these two:

• Discriminant of the icosahedral group.

• Discriminant of restricted of quintic.

In his remarkable book The Theory of Singularities and its Applications, Vladimir Arnol’d explains how the symmetry group of the icosahedron is secretly lurking in the problem of finding the shortest path from one point to another in a region of the plane with smooth boundary. Via Huygen’s principle, this shortest path problem is then related to the behavior of waves in such a region.

Arnol’d nicely expresses the awe mathematicians feel when they discover connections like this:

Thus the propagation of waves, on a 2-manifold with boundary, is controlled by an icosahedron hidden at an inflection point at the boundary. This icosahedron is hidden, and it is difficult to find it even if its existence is known.

In explaining this, Arnol’d starts by claiming that a generic involute of the cubical parabola has cusps of orders 3/2 and 5/2. There is a lot of terminology here, so let us try to explain it.

The cubical parabola

The cubical parabola is simply the curve \(y = x^3\), or any curve obtained from this by an affine transformation.

Involutes

An involute of a plane curve \(C\) is a new plane curve \(D\) obtained by attaching one end of a taut string to a point \(p\) on \(C\) and tracing the path of the string’s free end as you wind the string onto \(C\). There are different involutes for different choices of \(p\).

For example, here is a curve and one of its involutes:

Here \(C\), in blue, is a catenary: the curve formed by a hanging chain. An involute \(D\) of the catenary is shown in red.

There are two things about this picture that may be confusing at first. First, Sam Derbyshire, who made this picture, cleverly moved the end of the string attached to the catenary at the instant its free end hit the catenary! That allowed him to continue the involute past the moment it hits the catenary. The result is a curve called a tractrix.

Second, the end of the string attached to the catenary is ‘at infinity’.

These issues are handled more systematically by giving a formula for the involutes of a curve. Suppose a smooth plane curve is given in parametric form

$$C :\mathbb{R} \to \mathbb{R}^2$$

parametrized by arclength, so that

$$|C'(s)|=1$$

for all \(s\). Then for each \(t \in \mathbb{R}\), this curve has an involute

$$D_t :\mathbb{R} \to \mathbb{R}^2$$

given by

$$D_t(s) = C(s+t)- s C^\prime(s+t) $$

Cusps

If a plane curve looks locally like

$$y^2 = x^3$$

in some coordinates, we say it has a cusp of order 3/2 or ordinary cusp. If it looks locally like

$$y^2 = x^5$$

in some coordinates, we say it has a cusp of order 5/2 or rhamphoid cusp.

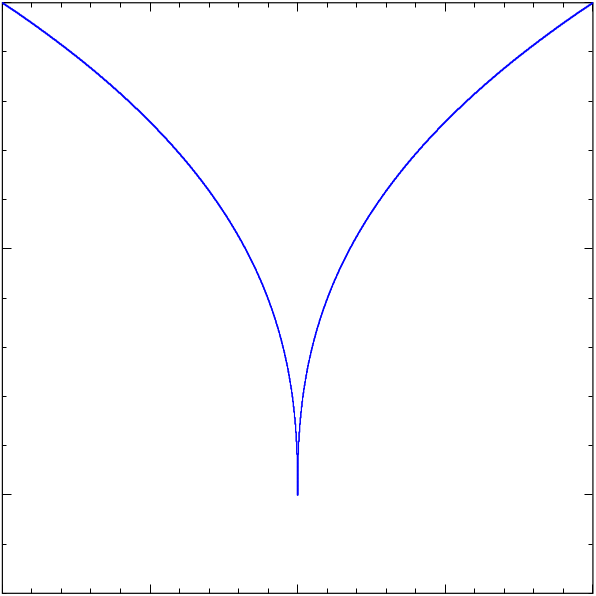
The curve \(y^2 = x^5\) looks like this:

This is a more typical curve with a cusp of order 5/2:

$$ (x-4y^2)^2 – (y+ 2x)^5 = 0 $$

It looks a bit like a bird’s beak:

Indeed, the word ‘rhamphoid’ means ‘beak-like’ in Greek. Arnol’d emphasizes that one should usually expect a cusp of order 5/2 to have such a beak-like shape:

It is easy to recognize this curve in experimental data, since after a generic diffeomorphism the curve consists of two branches that have equal curvatures at the common point, and hence are convex from the same side [….]

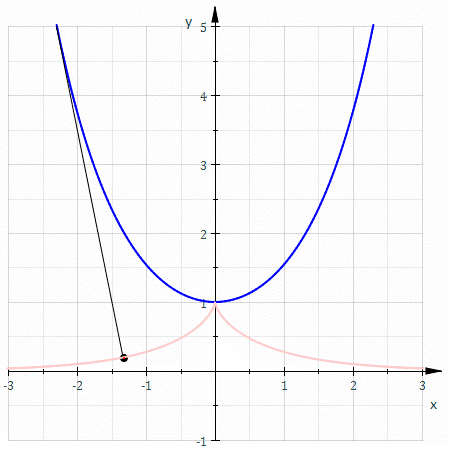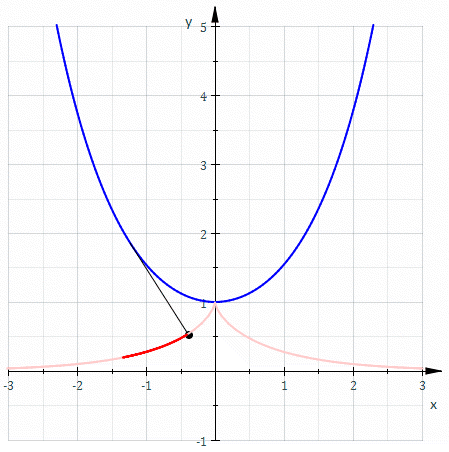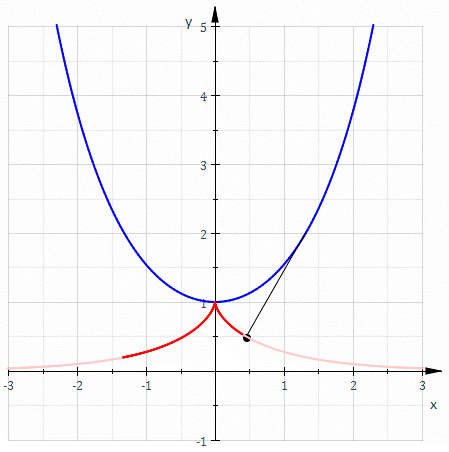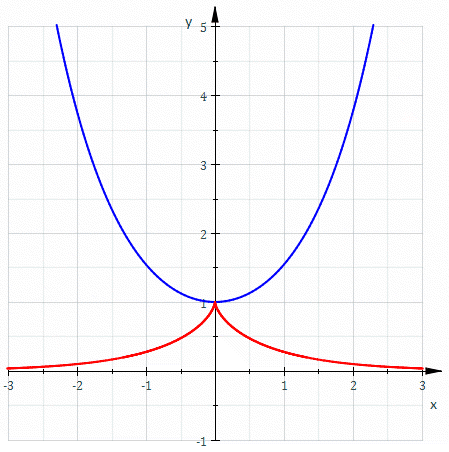
The involutes of a cubical parabola

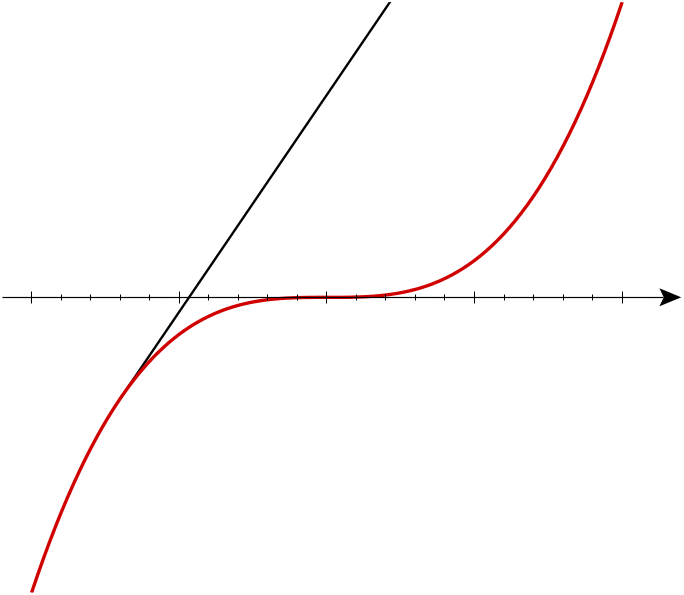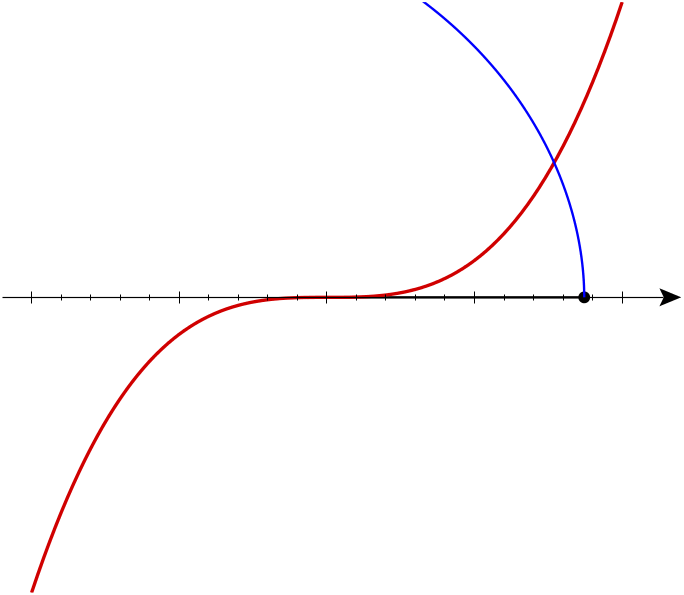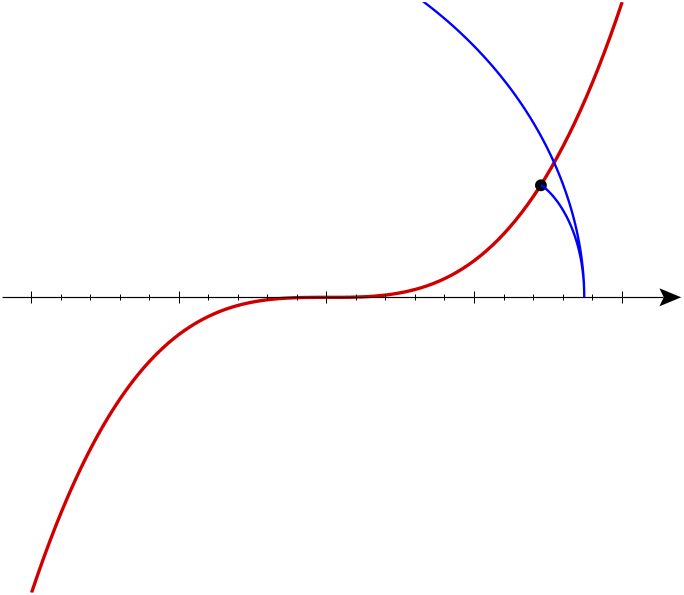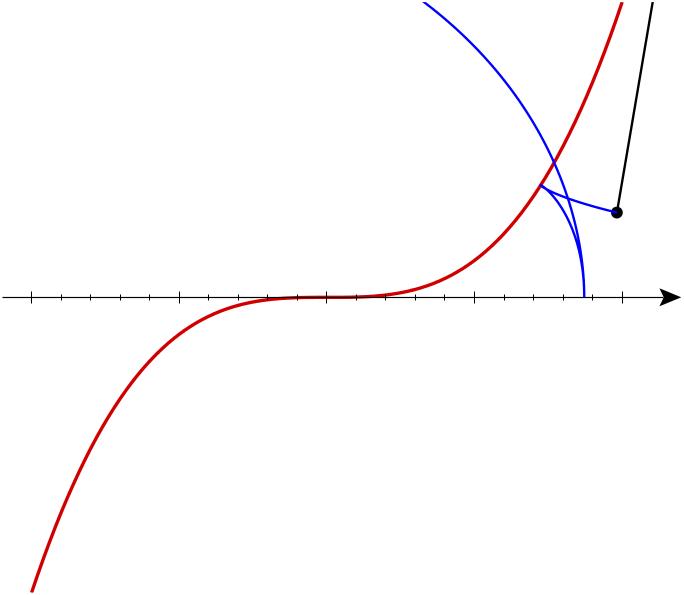
We can now understand Arnol’d’s remark that a generic evolute of the cubical parabola has cusps of orders 3/2 and 5/2:

The red curve is the cubical parabola \(y = x^3\). The moving blue curve shows all the involutes of the cubical parabola. Generically, each involute has a cusp of order 5/2 where it hits the \(x\) axis. Note that both branches are convex from the same side. Generically, each involute also has a cusp of order 3/2 where it hits the cubical parabola. The only non-generic case is the involute that passes through the origin. At the origin this involute has a singularity of order 5/3: that is, it is locally diffeomorphic to the curve \(y^3 = x^5\).

Simon Burton has drawn a detailed picture of a single generic involute, showing clearly how the cusps arise:

You can explore involutes of various curves online here:

• Marshall Hampton, SageMathCell

References

For more details, see pages 28–31 of this book:

• Vladimir I. Arnol’d, The Theory of Singularities and its Applications, Cambridge U. Press, Cambridge, 1991.

and page 169 in the English version of the following paper, or page 143 in the original Russian version, which is open-access:

• Vladimir I. Arnol’d, Singularities of systems of rays, Uspekhi Mat. Nauk 38:2 (1983), 77-147. English translation in Russian Math. Surveys 38:2 (1983), 77–176.

Also see section III of this paper:

• O. Y. Lyashko, Classification of critical points of functions on a manifold with singular boundary, Funktsional. Anal. i Prilozhen. 17:3 (1983), 28—36. English translation in Functional Analysis and Its Applications 17:3 (1983), 187–193

and these papers by Shcherbak:

• O. P. Shcherbak, Singularities of a family of evolvents in the neighbourhood of a point of inflection of a curve, and the group \(\mathrm{H}_3\) generated by reflections, Funktsional. Anal. i Prilozhen. 17:4 (1983), 70–72. English translation in Functional Anal. Appl. 17:4 (1983), 301–303.

• O. P. Shcherbak, Wavefronts and reflection groups, Uspekhi Mat. Nauk 43:3 (1988), 125–160. English translation in Russian Mathematical Surveys 43:3 (1988), 1497–194.

These sources discuss the discoveries of Arnol’d and his colleagues relating singularities and Coxeter–Dynkin diagrams, starting with the more familiar \(\mathrm{ADE}\) cases, then moving on to the non-simply-laced cases, and finally the non-crystallographic cases related to \(\mathrm{H}_2\) (the symmetry group of the pentagon), \(\mathrm{H}_3\) (the symmetry group of the icosahedron) and \(\mathrm{H}_4\) (the symmetry group of the 600-cell).

The animated gif of the tractrix as an involute of the catenary was created by Sam Derbyshire and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!