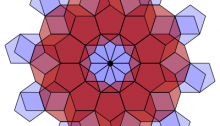
Branched Cover from (4 4 3/2) Schwarz Triangle
A Schwarz triangle is a spherical triangle that can be used to generate a tiling of a branched covering of the sphere by repeatedly reflecting this triangle across its edges. Sometimes we get an actual tiling of the sphere, but in general we get a branched covering, because the same point can lie in the interior of several triangles, and there may be branch points at the corners of the triangles.