Two regular pentagons and a regular decagon fit snugly at a point: their interior angles sum to 360°. Despite this, you cannot tile the plane with regular pentagons and decagons:

• Pentagon-decagon packing.

However, there is a branched covering of the plane tiled with pentagons and decagons that map to regular pentagons and decagons on the plane!

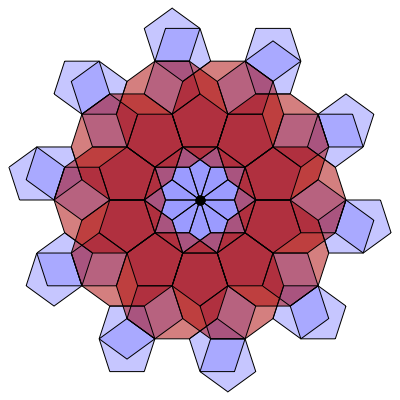
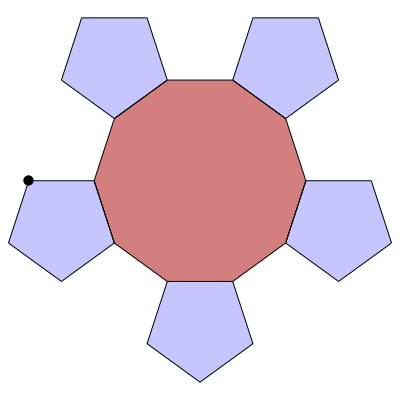
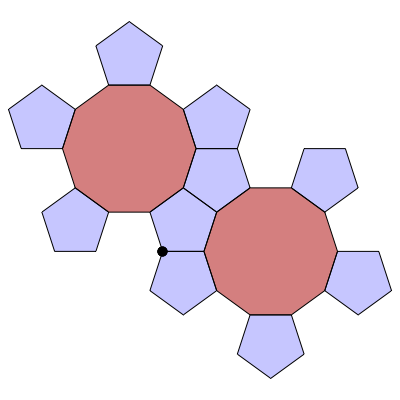
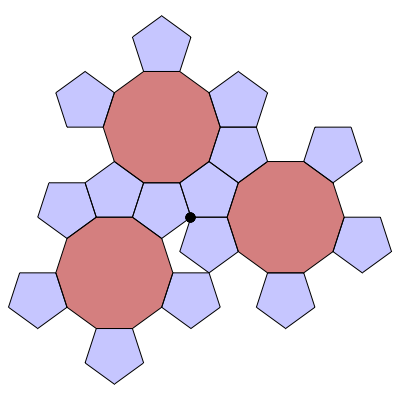
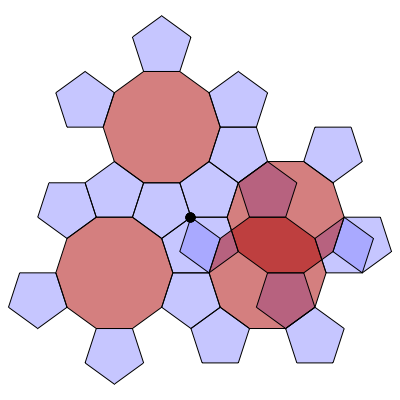
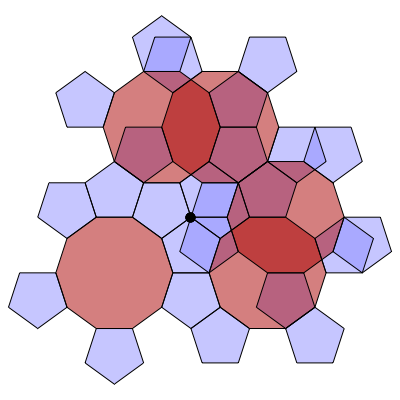
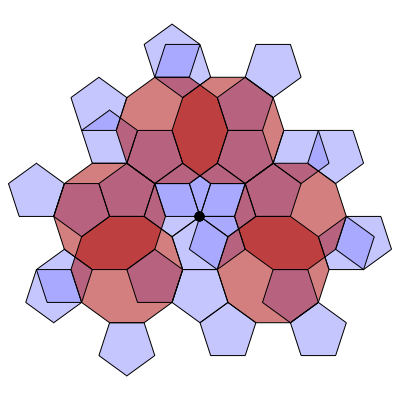
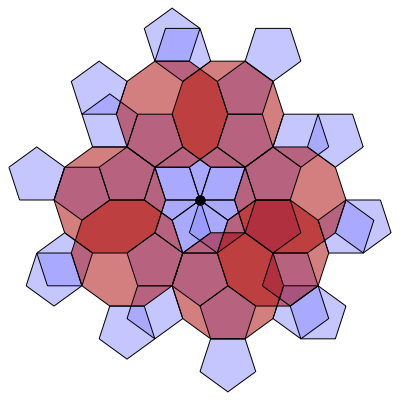
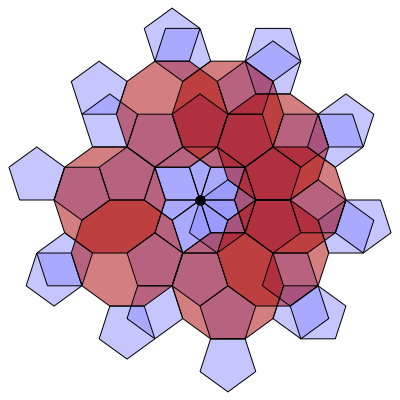
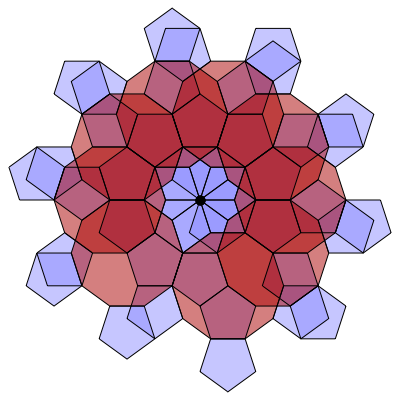
In the following series of images by Greg Egan, we see how to build up this branched covering. The basic unit is a decagon with a pentagon attached to every other edge. You can glue these units together along their edges, and end up with 10 pentagons meeting at a branch point (the black dot):

Since the interior angle of a regular pentagon on the plane is \( 3\pi/5 \), the total interior angle at the branch point is

$$ 10 \times 3\pi/5 = 3 \times 2 \pi $$

Thus we obtain a branch point of ramification index 3. In other words, our surface maps to the Euclidean plane in a way that looks locally the same as the Riemann surface for the function \( z^{1/3} \).

If we continue gluing on more units of type, we obtain a surface tiled by pentagons and decagons. In this surface, each decagon touches 10 pentagons along its edges. Each pentagon touches 2 decagons and 3 pentagons along its edges. There are two kinds of vertices. At some vertices, 2 pentagons and a decagon meet. At others, 10 pentagons meet.

This surface can be given a conformal structure, by defining angles between tangent vectors just as usual for points in the interiors of pentagons and decagons, or along their edges, or at vertices where 2 pentagons and a decagon meet—but rescaling angles at vertices where 10 pentagons meet, dividing by 3 to make the total angle $2 \pi$.

This makes our surface into a Riemann surface, that is, a 1-dimensional complex manifold. In fact, we can show that it is biholomorphic to the hyperbolic plane $\mathcal{H}$, and its map to the Euclidean plane

$$ p \colon \mathcal{H} \to \mathbb{C} $$

is holomorphic, with infinitely many branch points, all of ramification index 3. These branch points are dense in \(\mathbb{C}\).

Even better, there is an infinite discrete group acting as isometries of the Euclidean plane \(\mathbb{C}\) and also of hyperbolic plane \(\mathcal{H}\), with the property that \(p\) respects these symmetries:

$$ p(g x) = g p(x) $$

for every \(x \in \mathcal{H}\) and group element \(g\). This group is the Coxeter group

More or less by definition, this is the symmetry group of a tiling of the hyperbolic plane by equal-sized regular pentagons where 10 meet at each vertex.

Why are all these things true? To see why, start by tiling \(\mathcal{H}\) with equal-sized regular pentagons where 10 meet at each vertex. This tiling, called the {5,10} tiling, is unique up to isometries of \(\mathcal{H}\). Note that the interior angles of these pentagons are not \(3 \pi / 5\), but \(\pi/5\).

Let \(p : \mathcal{H} \to \mathbb{C}\) be a holomorphic map that sends each of these pentagons to a regular pentagon in the complex plane with its usual Euclidean metric. This map is unique up to isometries of \(\mathbb{C}\), and it has a branch point of order 3 at each pentagon vertex. Thus, the interior angles of the pentagons in the hyperbolic plane get tripled when they are mapped via \(p\) to the Euclidean plane.

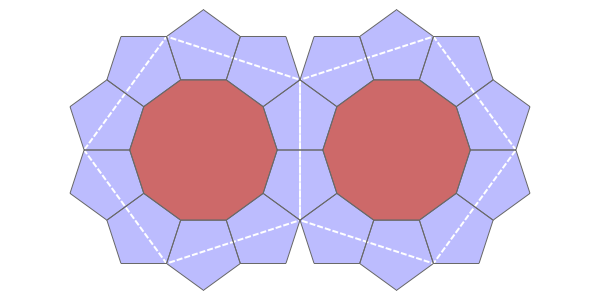
Subdivide each pentagon in the Euclidean plane as follows:

Lifting this subdivision to a subdivision of the pentagons in \(\mathcal{H}\), we obtain a way of tiling \(\mathcal{H}\) by regions conformally equivalent to decagons and pentagons. (Beware: the edges of these regions in \(\mathcal{H}\) are not geodesics, unlike the larger pentagons they were created from. Only their images in \(\mathbb{C}\) have straight lines as edges: these are regular decagons and pentagons in the plane.)

Since we have now constructed the map

$$ p \colon \mathcal{H} \to \mathbb{C} $$

starting from just the tiling of \(\mathcal{H}\) by equal-sized regular pentagons with 10 meeting at each vertex, without making any choices that break the symmetry, we can now conclude that the Coxeter group

acts as isometries of the Euclidean plane \(\mathbb{C}\) and also of hyperbolic plane \(\mathcal{H}\), and that

$$ p(g x) = g p(x). $$

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!