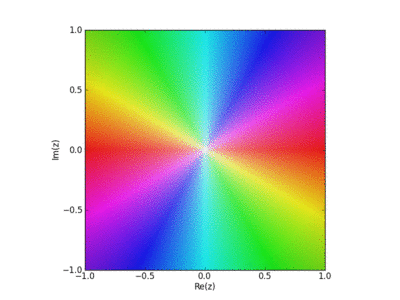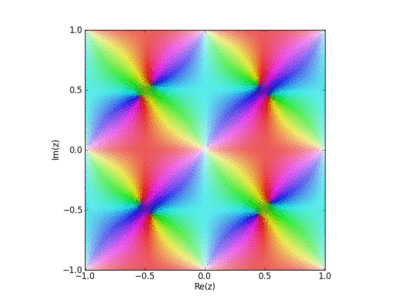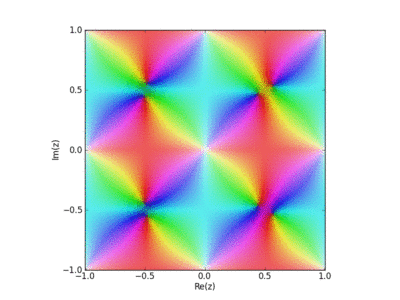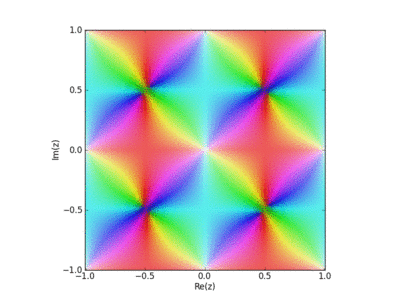
Here David Chudzicki shows how the Weierstrass elliptic function is built up as a sum of terms, one for each point in a lattice in the complex plane. Each term has a pole at one lattice point. The resulting function is periodic in two directions and analytic except for poles at the lattice points. The phase of this function is shown using color, and its magnitude using brightness.

More precisely, choose two complex numbers $\omega_1, \omega_2$ that are linearly independent when considered as vectors in the plane $\mathbb{R}^2$. The set

$$ L = \{ m \omega_1 + n \omega_2 : \; m, n \in \mathbb{Z} \}$$

is called a lattice. A first attempt at defining the Weierstrass elliptic function would be

$$ \sum_{\omega \in L} \frac{1}{(z – \omega)^2} $$

but this sum diverges. So, we subtract a term $1/\omega^2$ for each point $\omega$ in the lattice $L$, except of course for $\omega = 0$. The result is the Weierstrass elliptic function:

$$ \wp(z) = \frac{1}{z^2} + \sum_{\omega \in L- \{0\}} \frac{1}{(z – \omega)^2} – \frac{1}{\omega^2} .$$

This is analytic except for poles of order two at the points in the lattice $L$, and it is periodic in the following sense:

$$ \wp(z + \omega) = \wp(z) $$

whenever $\omega \in L$.

In David Chudzicki’s movie, he takes the square lattice with

$$ \omega_1 = 1, \quad \omega_2 = i $$

Here is a zoomed-in version of this movie:

You can see the function getting closer and closer to periodic with each extra term.

Chudzicki has a blog article on these movies, and he’s put them and the code for them in the public domain:

• David Chudzicki, Weierstrass elliptic function; movies and code.

The Weierstrass elliptic function is very important in the theory of elliptic curves. For an explanation, see:

• John Baez, This Week’s Finds in Mathematical Physics (Week 13).

This also explains why we need to sum terms like

$$ \frac{1}{(z – \omega)^2}$$

instead of the simpler

$$ \frac{1}{(z – \omega)} .$$

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!