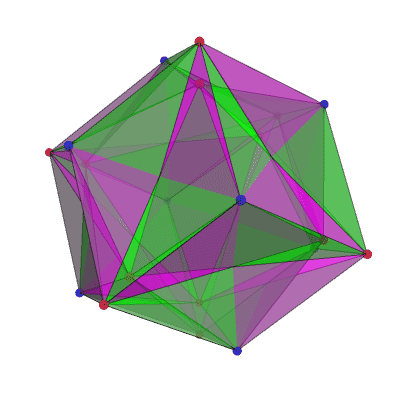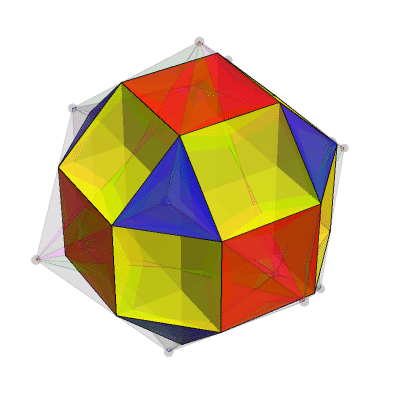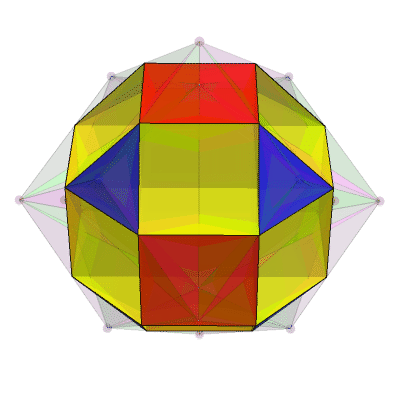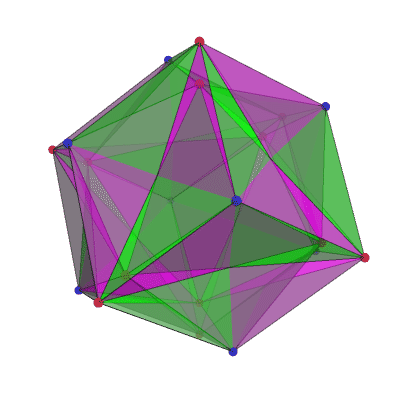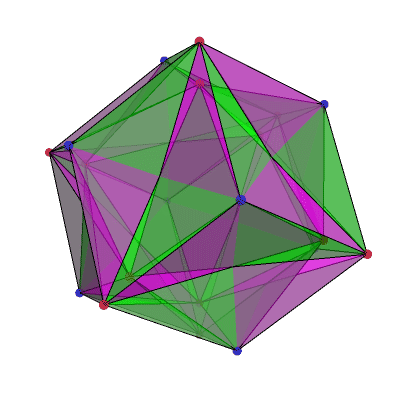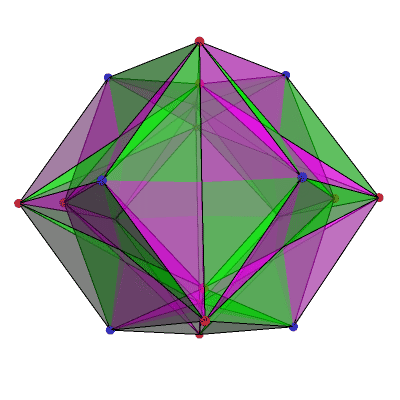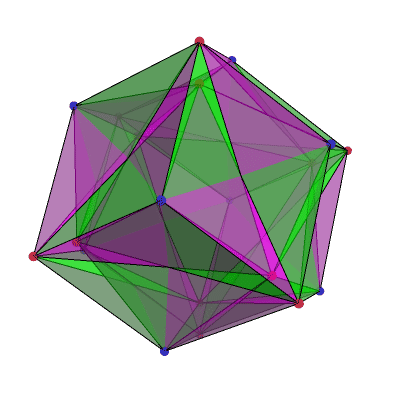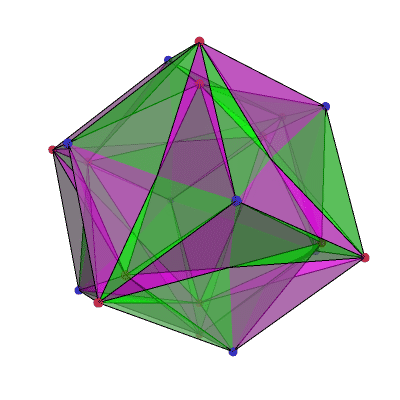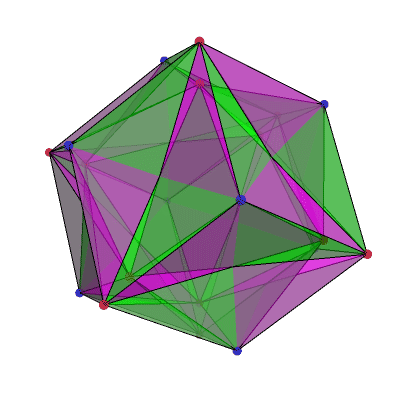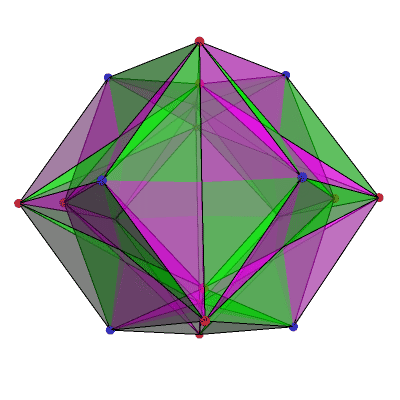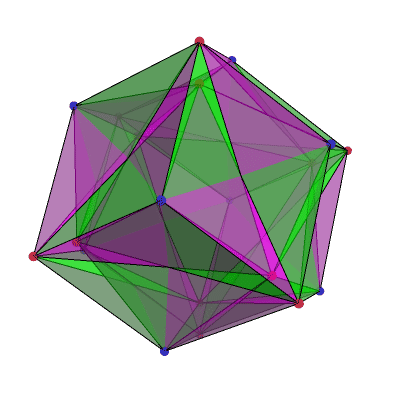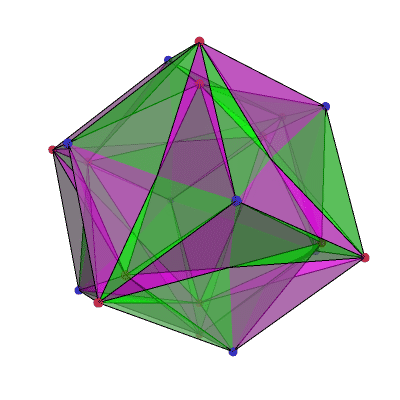
Branched Cover from (4432) Schwarz Triangle – Greg Egan
A Schwarz triangle is a spherical triangle that can be used to generate a tiling of a branched covering of the sphere by repeatedly reflecting this triangle across its edges. Sometimes we get an actual tiling of the sphere, but in general we get a branched covering, because the same point can lie in the interior of several triangles, and there may be branch points at the corners of the triangles.
A Schwarz triangle is specified by three rational numbers, written (pqr), each representing the interior angle at one vertex of the triangle. The number p stands for the angle π/p, and so on.
This image by Greg Egan shows the tiling that arises from the (4432) Schwartz triangle. This is an isosceles spherical triangle with angles π/4, π/4 and 2π/3, or 45°, 45° and 120°. 48 of these triangles tile a branched covering of the sphere by a 3-holed torus.
You can also get this branched covering by taking a polyhedron called the ‘small cubicuboctahedron’ and projecting its surface to the surface of a sphere.
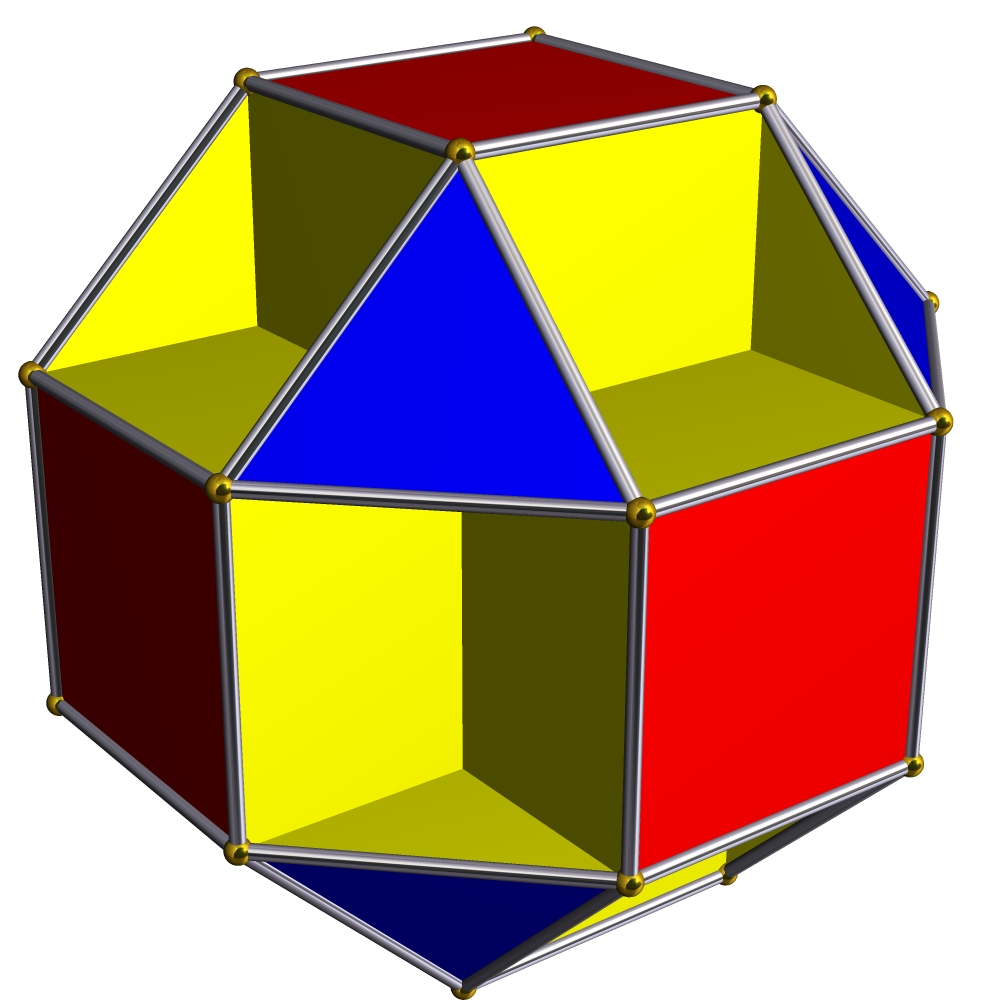
Small Cubicuboctahedron – Robert Webb
We discussed this polyhedron last time:
• Small cubicuboctahedron.
To see how the small cubicuboctahedron and the tiling by (4432) Schwartz triangles are related, look at this movie created by Egan:
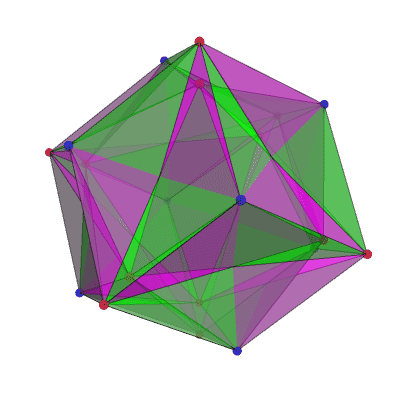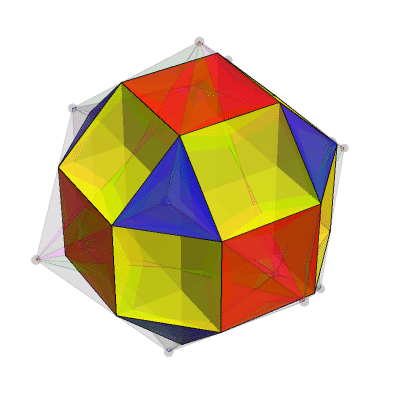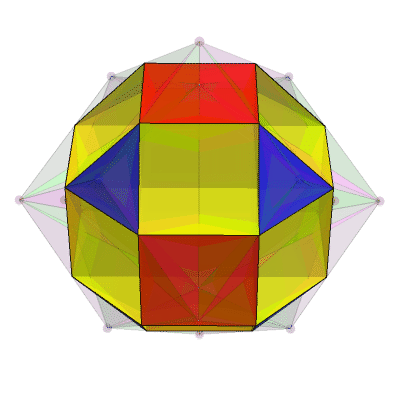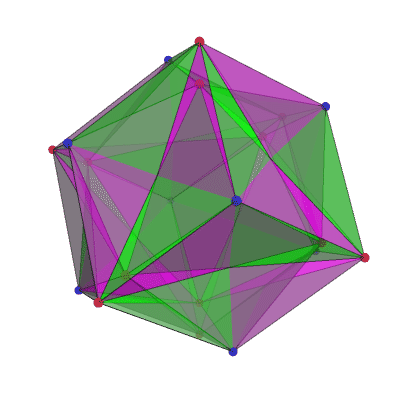
Small Cubicuboctahedron from Genus 3 Branched Cover – Greg Egan
Here are some details on the tiling, written by Egan:
If you divide each face of an octahedron (construed as a spherical triangle, not a flat one!) into three isosceles triangles, with edges of the octahedron as the base of each triangle and the centre of the face as the apex, those triangles have angles of 2π/3 at the apex and π/4 at the other two corners.
These isosceles triangles cover two of the 48 fundamental domains of the 48-element cubic symmetry group, so the cover has density 2. There is a branch point of order 2 at the centre of each face of an octahedron; although three triangles fit perfectly around each face, the rule is that you need an even number of reflections around any cycle, so there must be 6 triangles around each face-centre. That gives a total of 20 vertices in the tiling: 8 from the octahedron face-centres, plus twice the number of octahedron vertices, 2 x 6 = 12, because there are two distinct sheets sitting over those points. This gives us an Euler characteristic:
χ=48–(3/2)×48+20=−4
which is (2−2g) for g=3. So, this surface has genus 3.
We can tile the hyperbolic plane with isosceles triangles of this type, giving a covering space of the genus-3 surface:

Hyperbolic Plane Tiled by (4 4 3/2) Schwarz Triangles – Greg Egan
The image of the small cubicuboctahedron was placed on Wikimedia Commons by Tom Ruen, and the copyright holder of this file allows anyone to use it for any purpose, provided that acknowledgement is given to Robert Webb’s Great Stella software as the creator of this image along with a link to the Stella website.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!