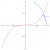
The ambidextrous moving sofa problem is to find the planar shape of maximal area that can negotiate right-angled turns both to the right and to the left in a hallway of width 1. The current best known solution was found by Dan Romik, and is shown here.
Romik’s ambidextrous sofa has a boundary consisting of 18 curves, each described by a separate formula. Some of these curves are portions of circles, while the rest are portions of sextics: that is, curves described by polynomials of degree 6. The area of Romik’s ambidextrous sofa is x+arctanyx+arctany, where x and y are solutions to the cubic equations x2(x+3)=8 and y(4y2+3)=1. More explicitly, its area is:
3√3+2√2+3√3−2√2−1+arctan[12(3√√2+1−3√√2−1)]≈
1.644955218425440…
Nobody has proved his solution is optimal. We’re not even sure that it’s locally optimal, meaning that you can’t make slight changes in his shape that increase the area and get a shape that still fits down the hallway. This is an interesting challenge.
For a closer look at how Romik’s sofa slides down the hallway, complete with a subdivision of its boundary into 18 pieces, see this:
• Dan Romik, The new ambidextrous sofa — sofa-centric view.
It is worthwhile comparing our previous article:
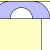
The Hammersley sofa is an early attempt to solve the moving sofa problem posed by Leo Moser in 1966:
What’s the largest possible area of a 2-dimensional region that can be maneuvered using rigid motions through an L-shaped hallway of width 1?
Romik explains some of the history:
Around the time that the moving sofa problem was first published, John H. Conway, G. C. Shepard and several other mathematicians were said to have worked on the problem during a geometry conference, as well as on several other variants of the problem, each of which was apparently assigned to one member of the group. We now consider one of these variants, which asks for the planar shape of maximal area that can negotiate right-angled turns both to the right and to the left in a hallway of width 1. We refer to this as the ambidextrous moving sofa problem. The Conway et. al.~ arly attack led to two rough guesses about the approximate shape of the solution, nicknamed the “Conway car” and “Shepard piano”. The problem was considered again in 1973 by Maruyama, who developed a numerical scheme for computing polygonal approximations to the problem and several other variants. More recently, in a 2014 paper Gibbs developed another numerical technique to study the problem, and computed a similar-looking shape (in much higher resolution), whose area he calculated to be approximately 1.64495.
Here I have omitted references to papers and figures that appear in Romik’s paper:
• Dan Romik, Differential equations and exact solutions in the sofa problem, 2016.
He also has a nice webpage about moving sofa problems:
• Dan Romik, The moving sofa problem.
The papers by Maruyama and Gibbs are these:
• K. Maruyama, An approximation method for solving the sofa problem, Int. J. Comp. Inf. Sci. 2 (1973), 29–48.
• Philip Gibbs, A computational study of sofas and cars, 2014.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

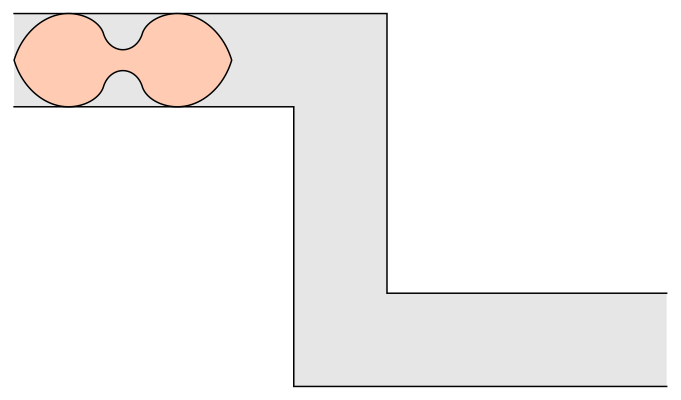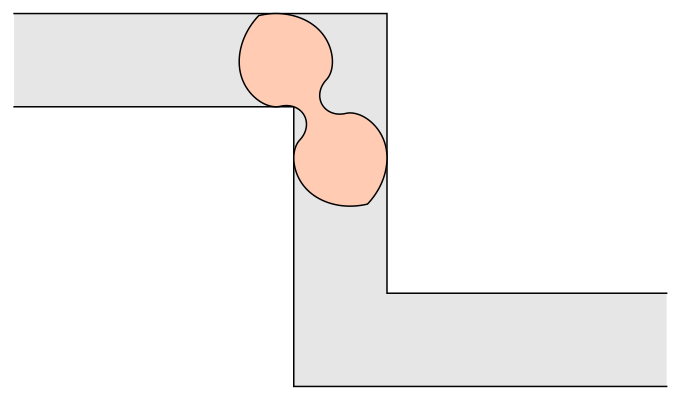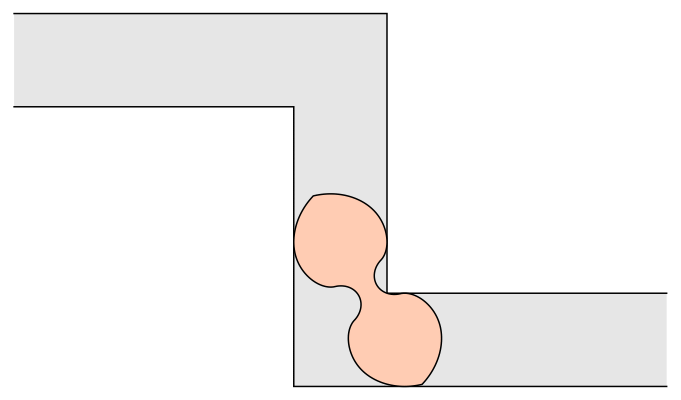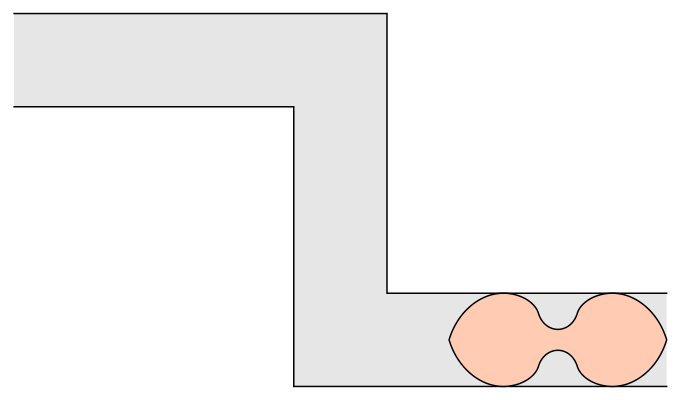

Is it also possibile to move the sofa using rotations and translations?
Now the hard part of the problem: finding someone who wants that thing in their living room! Maybe if it was a barbell instead of a sofa…
I wonder if this explains the shape of red blood cells, which must pass thru tiny capillaries?
the cross section of a red blood cell, if you cut it in half, looks similar to this.