
Small Stellated Dodecahedron – Robert Webb’s Stella software
The small stellated dodecahedron is made of 12 pentagrams, or 5-pointed stars, with 5 pentagrams meeting at each vertex. It is one of four nonconvex polyhedra with regular polygons or stars as faces, called Kepler–Poinsot polyhedra.
The small stellated dodecahedron was studied by Kepler. It appears in his Harmonice Mundi, published in 1619. However, it also can be found in a floor mosaic in St Mark’s Basilica in Venice, which seems to have been created by Paolo Uccello as early as 1430.

Floor Mosaic, St Mark’s Basilica, Venice – Paolo Uccello
Later it was used by Escher in two of his prints: Constrast: Order and Chaos and Gravitation.
The small stellated dodecahedron and other Kepler–Poinsot solids posed a challenge to early topologists. If we treat the small stellated dodecahedron as having 12 five-sided faces, two meeting along each edge, then it should have 12×5/2=30 edges. Since it has 12 vertices as well, its Euler characteristic should be
χ=V–E+F=12–30+12=–6
Since the genus g of a surface is related to its Euler characteristic by χ=2–2g, the small stellated dodecahedron should have genus 4! This was first noted by Poinsot, and it caused some confusion about the validity of Euler’s formula V–E+F=2, which we now realize holds only for convex polyhedra.
However, we can in fact treat the small stellated dodecahedron as the image of a continuous map from a surface Σ of genus 4 into three-dimensional space. This map has branch points of order 2 at the center of each pentagram, hidden from view in the picture!
Indeed, if we think of the stellated dodecahedron as defining a branched cover of the sphere, this branched cover becomes a Riemann surface. The orientation-preserving symmetries of the icosahedron clearly act as conformal transformations of this Riemann surface. It thus has at least the alternating group A5 as symmetries.
This was observed by Klein in 1877:
• Felix Klein, Weitere Untersuchungen über das Ikosaeder, Math. Annalen 12 (1877), 321–384.
The Riemann surface Σ can be tiled by 12 pentagons, 5 meeting at each corner. These correspond to the 12 pentagrams of the small stellated dodecahedron. Thanks to this tiling, Σ can also be thought of as a quotient of the hyperbolic plane H2 by a discrete group Γ acting as isometries. This group preserves a tiling of the hyperbolic plane by regular hyperbolic pentagons, 5 meeting at each corner:
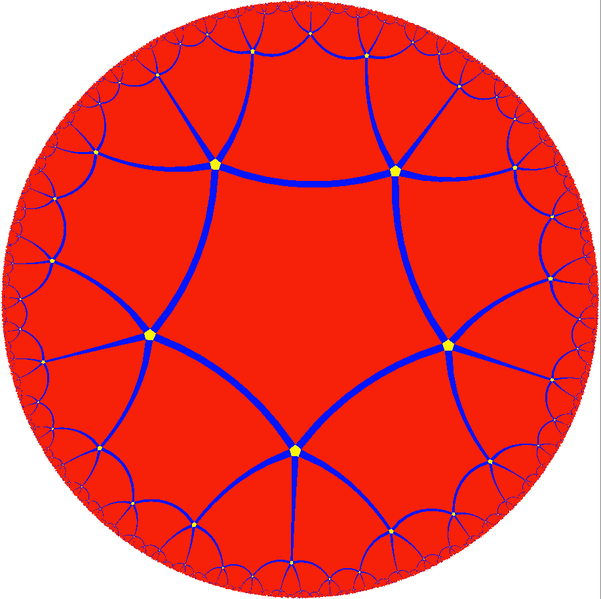
{5,5} Tiling – Jeff Weeks
This tiling of the hyperbolic plane is called the {5,5} tiling.
The small stellated dodecahedron is the image of a certain map from the Riemann surface Σ into R3. But this surface can also be mapped into R3 in a different way, giving another Kepler–Poinsot polyhedron, the great dodecahedron:

Great Dodecahedron – Robert Webb’s Stella Software
This should not be surprising, because the great dodecahedron has 12 pentagonal faces, 5 meeting at each vertex. However, the ultimate explanation is that the great dodecahedron is the dual of the small stellated dodecahedron — the vertices of one lie at the centers of the faces of the other — and the {5,5} tiling is its own dual!
For more on the great dodecahedron see this post, which explains its connection to an exceptionally symmetrical code:
• Golay code.
The Riemann surface Σ also has an interesting connection to the quintic equation. A Riemann surface is also called a ‘complex curve’, since points on it can be locally described by a single complex number. Klein showed that Σ is isomorphic to the complex curve described by these homogeneous equations:
5∑i=1zi=0,5∑i=1z2i=0,5∑i=1z3i=0.
These three equations in five complex variables pick out a set of complex dimension two, but when we ‘projectivize’, identifying solutions that differ by a complex multiple, we obtain a complex curve embedded in the projective space CP4.
This is called as Bring’s curve, and it is famous because it has the largest possible symmetry group of any complex curve (or Riemann surface) of genus 4. In fact, this group is not just A5 but the symmetric group S5.
We can see that S5 acts as symmetries by relating Bring’s surface to the quintic equation. Consider a quintic of the form
Q(z)=(z−z1)⋯(z–z5)
If the three equations
5∑i=1zi=0,5∑i=1z2i=0,5∑i=1z3i=0
hold, then Q takes the special form
Q(z)=z5+pz+q.
Conversely, if Q takes this special form, its roots z1,…,z5 obey the three equations listed. Thus, Bring’s curve is the set of ordered 5-tuples (z1,…,z5), modulo scalar factors, that are roots of some quintic of the form z5+pz+q.
For more on these topics, see:
• Matthias Weber, Kepler’s small stellated dodecahedron as a Riemann surface, Pacific J. Math. 220 (2005), 167–182.
Abstract. We provide a new geometric computation for the Jacobian of the Riemann surface of genus 4 associated to the small stellated dodecahedron. Starting with Threlfall’s description, we introduce other flat conformal geometries on this surface which are related to holomorphic 1-forms. They allow us to show that the Jacobian is isogenous to a fourfold product of a single elliptic curve whose lattice constant can be determined in two essentially different ways, yielding an unexpected relation between hypergeometric integrals. We also obtain a new platonic tessellation of the surface.

Small Stellated Dodecahedron – Cyp
The featured picture of the small stellated dodecahedron was created using Robert Webb’s Stella software and placed on Wikicommons. The same is true of the picture of the great dodecahedron. Robert Webb allows anyone to use these pictures for any purpose, provided that the copyright holder is properly attributed. The picture of the floor mosaic in the Basilica of St Mark is from this page:
• George Hart, Paolo Uccello’s Polyhedra.
but is available on Wikicommons, where it is listed as being in the public domain. The picture of the {5,5} tiling was drawn by Tom Ruen using Jeff Week’s KaleidoTile software and placed in the public domain on Wikicommons. The rotating image of the small stellated dodecahedron was created by Cyp and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




This Riemann surface is supported by MagicTile, and so there are number of permutation (Rubik-like) puzzles you can play on it!
Here is a picture of one of them. The image is very much like the picture in section 2 of Weber’s paper, except with colors marking identifications rather than numbers.
https://goo.gl/photos/oC27H6h6yyzUz4VE9
Here is that same puzzle scrambled 🙂
https://goo.gl/photos/v8SHbisnkRVWTv5p9
If you have a Windows machine, you can download and play for free here: http://www.gravitation3d.com/magictile
Some of the pieces of my naive understanding of what you wrote don’t fit together, and I am curious about the gap. I assume “piecewise linear” (Riemannian metric) means the same as piecewise Euclidean in that context. Even if I assume that the metric induced by the immersion in R3 knows about the branch points of order 2, the interior angles at the tips of the pentagrams are still π/5, but since 5 pentagons meet at each vertex of the tiling in hyperbolic space, the interior angles of these pentagrams are 2π/5. So the angles aren’t preserved here, contradicting my interpretation of “conformal”. I guess it is conformal everywhere except at singularities at the vertices of the tessellation?
Good point. My comment didn’t really make sense, so I’ll fix it. You really need to do something else to see the conformal structure on the small stellated dodecahedron.
For example: project it radially onto the 2-sphere to get a kind of ’tiling’ of the 2-sphere by spherical pentagrams, which however overlap each other. Subdivide each spherical pentagram into 10 spherical right triangles.
These triangles have interior angles π/2 (since they are right triangles), 2π/5 (since ten triangles meet at the center of each pentagram but this is a branch point of order 2), and π/5 (since five pentagrams and thus ten triangles also meet at each ‘sharp tip’ of the small stellated dodecahedron). So, we call them (2,5/2,5) Schwarz triangles.
Each pentagram is covered by 10 triangles of this type, and there are 12 pentagrams, so we have achieved a kind of tiling of the Riemann sphere by 120 spherical triangles. However, these triangles overlap, so it’s not a tiling in the usual sense. They actually define a tiling of a branched covering of the Riemann sphere, with a branch point of order 2 at the center of each pentagram!
The interior angles of the triangles on the sphere are, as mentioned, π/2,2π/5 and π/5. The branched cover has 12 branch points of order 2, one at the center of each pentagram, so the interior angles 2π/5, lying at these points, get halved up on the branched cover.
So, our branched cover, called Bring’s curve, gets a Riemannian metric where it’s tiled by constant-curvature triangles with interior angles of π/2,π/5, and π/5. Since these angles add up to 9π/10, which is less than 180 degrees, these are not spherical triangles: they live naturally in hyperbolic space!
They are, in fact, the triangles you get by taking the {5,5} tiling of hyperbolic space (shown above) and subdividing each pentagon into 10 hyperbolic right triangles. These are isosceles right triangles!
Nice. Thank you, this is clear.
However, it seems there should be a conformal mapping, a kind of ‘piecewise stereographic projection’, from the actual small stellated dodecahedron down to the 2-sphere! I guess this only fails to be angle-preserving at the vertices. So my original idea was probably not completely wrong; I guess you spotted where it breaks down.
Right, it makes more sense in retrospect. Poking around the web reminds me that a space of constant curvature (e.g., the 2-sphere) is locally conformally flat, and a polyhedron is manifestly flat except at its vertices.
Right.
As you may know, some theorem or other says that every compact Riemann surface is conformally equivalent to one with a metric of constant positive curvature (if the surface is a topologically a sphere), vanishing curvature (if the surface is topologically a torus), or constant negative curvature (if the surface has higher genus). In the last case, which is the most exciting one, the surface with its constant-curvature Riemannian metric is the quotient of the hyperbolic plane by a discrete group acting as isometries.
However, every Riemann surface is locally conformally equivalent to a flat one. That is, no matter what the conformal structure, you can pick a Riemann metric that’s flat near your favorite point, or even on each polygon in a polygonal decomposition of the surface. This pushes the curvature to the vertices, where it’s manifested as an angle deficit. The sum of these angle deficits must be 2π times the genus of the surface.
The discriminant of is
is  . Thus, the discriminant of
. Thus, the discriminant of 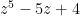 is zero, the discriminant of
is zero, the discriminant of 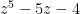 is zero, and the discriminant of
is zero, and the discriminant of  is 0. These are the only polynomials of the form
is 0. These are the only polynomials of the form  with discriminant zero. What points do these correspond to?
with discriminant zero. What points do these correspond to?