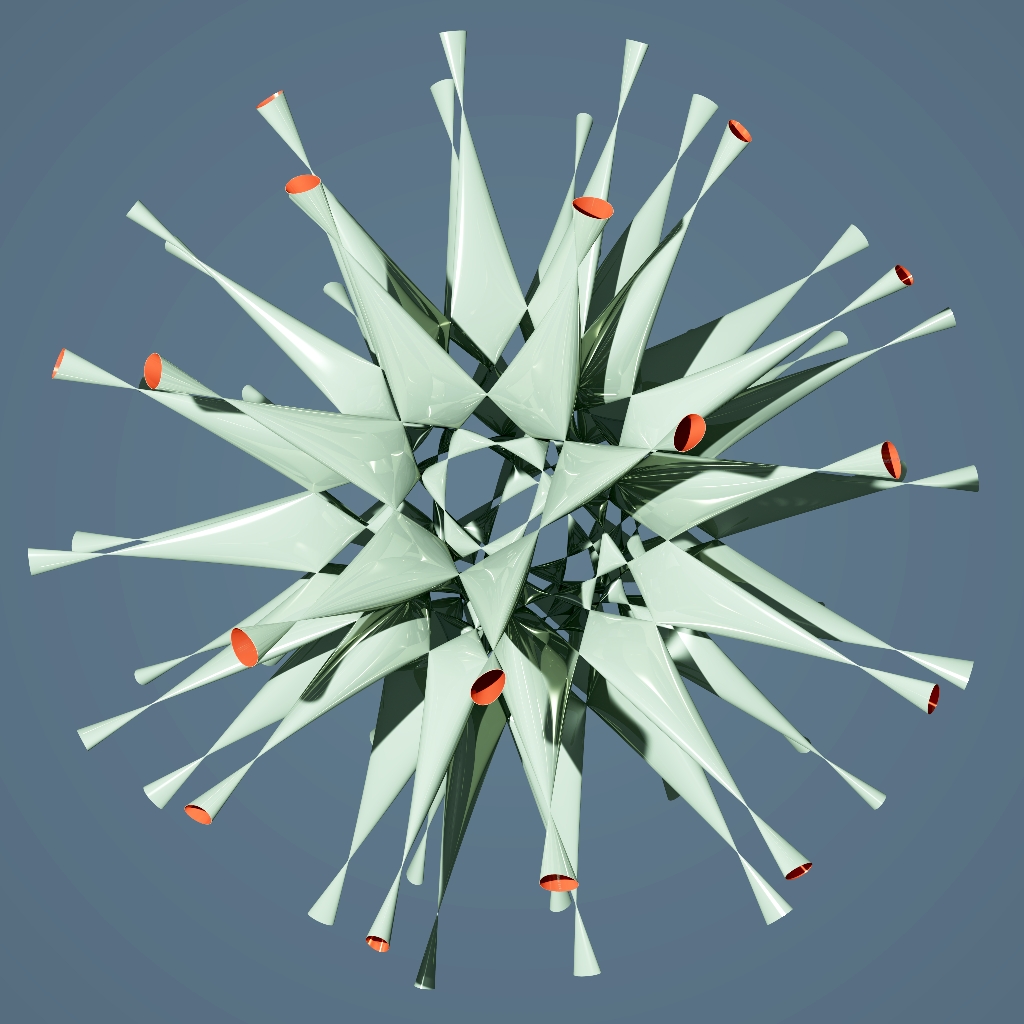
A decic surface is one defined by a polynomial equation of degree 10. The Barth decic, drawn above by Abdelaziz Nait Merzouk, is currently the decic surface with the largest known number of ordinary double points: that is, points where it looks like the origin of the cone in 3-dimensional space defined by

$$ x^2 + y^2 = z^2 .$$

It has 345 ordinary double points, while the best known upper bound for a decic surface that’s smooth except for such singularities is 360.

The Barth decic is defined by this homogeneous polynomial equation of degree 10 in four variables \(w,x,y,z\):

$$ \begin{array}{c} 8 (x^2 – \Phi^4 y^2) (y^2 – \Phi^4 z^2) (z^2 – \Phi^4 x^2) \left( x^4 + y^4 + z^4 – 2 x^2 y^2 – 2 x^2 z^2 – 2 y^2 z^2\right) \\
+ (3 + 5 \Phi) w^2 \left( x^2 + y^2 + z^2 – w^2 \right)^2 \left( x^2 + y^2 + z^2 – (2-\Phi)^2 w^2)\right) = 0 \end{array} $$

where

$$ \Phi = \frac{\sqrt{5} + 1}{2} $$

is the golden ratio. This equation determines a subset \(S \subset \mathbb{C}^4\) with complex dimension 2. Note that if \((w, x, y, z \in \mathbb{C}^4 \) is a solution, so is any multiple \((cw, cx, cy, cz) \). We may thus projectivize \(S\), treating any solution as ‘the same’ as any multiple of that solution. The result is an algebraic variety \(X\) in the complex projective space \(\mathbb{C}\mathrm{P}^3\). This variety has complex dimension 2, so it is called a complex surface. To obtain an ordinary real 2-dimensional surface we may take its intersection with a copy of \(\mathbb{R}\mathrm{P}^3\) in \(\mathbb{C}\mathrm{P}^3\).

Sitting inside \(\mathbb{R}\mathrm{P}^3\) we in turn have many copies of ordinary 3-dimensional space, \(\mathbb{R}^3\). The picture above shows the portion of the Barth decic living in one of these copies. Concretely, this consists of real solutions of the above equation where \(w = 1\).

But we also have ‘points at infinity’. If you march off in either of two opposite directions in \(\mathbb{R}^3\), you will approach one of these points at infinity. The points at infinity form a projective plane, that is, a copy of \(\mathbb{R}\mathrm{P}^2\). Concretely, these points at infinity are the points in \(\mathbb{R}\mathrm{P}^2\) coming from points \((x,y,z,w) \in \mathbb{R}^4\) with \(w = 0\).

The Barth decic has 345 ordinary double points. However, 45 of these are points at infinity, so they are not visible in the above picture, or this one:

We can bring the double points at infinity into view by rotating \(\mathbb{R}\mathrm{P}^3\) slightly. If we slice the resulting surface to see it better, we obtain a picture like this:

We can also compress \(\mathbb{R}^3\) into a ball, so that the points at infinity lie on the surface of this ball. More precisely, the surface of this ball is a 2-sphere, a double cover of \(\mathbb{R}P^2\), so any antipodal pair of points in this 2-sphere correspond to the same point at infinity.

This gives the following view of the Barth decic:

You can see visually that the compressed Barth decic meets the 2-sphere in 10 great circles. To see this mathematically, we can take the equation for the Barth decic and set \(w = 0\):

$$ \begin{array}{c} (x^2 – \Phi^4 y^2) (y^2 – \Phi^4 z^2) (z^2 – \Phi^4 x^2) \left( x^4 + y^4 + z^4 – 2 x^2 y^2 – 2 x^2 z^2 – 2 y^2 z^2\right) = 0 \end{array} $$

This factors into 10 linear functions:

$$ (x – \Phi^2 y)(x + \Phi^2 y)(y – \Phi^2 z)(y + \Phi^2 z)(z – \Phi^2 x)(z + \Phi^2 x)(x-y-z)(x+y-z)(x-y+z)(x+y+z) = 0 $$

Each of these defines a plane in $\mathbb{R}^3$ whose intersection with the unit 2-sphere is one of the 10 great circles. These 10 great circles are orthogonal to the lines going through the opposite corners of a regular dodecahedron:

You can see 5 double points in each face of the dodecahedron and 1 at the midpoint of each edge, for a total of \(5 \times 12 + 30 = 90\). However, antipodal points on the sphere count as the same point at infinity, so we get a total of \(90/2 = 45\) double points at infinity.

For more related pictures see:

• Abdelaziz Nait Merzouk, Barth decic and dodecahedron.

It is worth comparing the Barth sextic:

• Barth sextic.

The group of rotation and reflection symmetries of an icosahedron, \(\mathrm{A}_5 \times \mathbb{Z}/2\), acts as symmetries of both the Barth sextic and the Barth decic. Barth introduced these surfaces here:

• Wolf Barth, Two projective surfaces with many nodes, admitting the symmetries of the icosahedron, Journal of Algebraic Geometry 5 (1994), 173–186.

Ordinary double points are also known as nodes. In 1984, Miyaoka proved that a decic surface in $\mathbb{C}\mathrm{P}^3$ with only rational double points can have at most 360 such points:

• Y. Miyaoka, The maximal number of quotient singularities on surfaces with given numerical invariants, Math. Ann. 268 (1984), 159–171.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!