You’ve probably tried to move a sofa around a bend in a hallway. It’s annoying. But it leads to some interesting math puzzles. Let’s keep things simple and work in 2 dimensions. Then the moving sofa problem asks:

What’s the largest possible area of a 2-dimensional region that can be maneuvered using rigid motions through an L-shaped hallway of width 1?

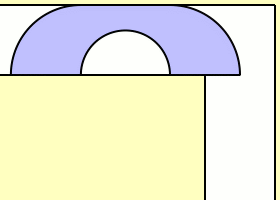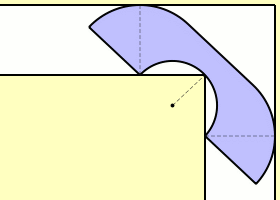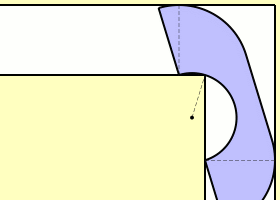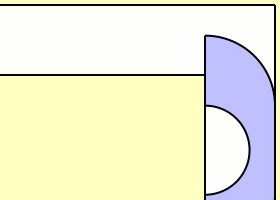
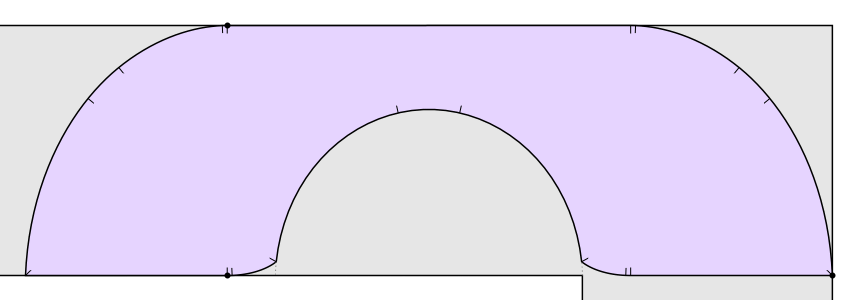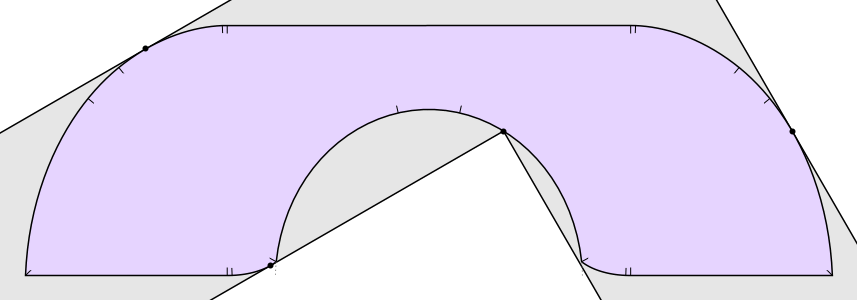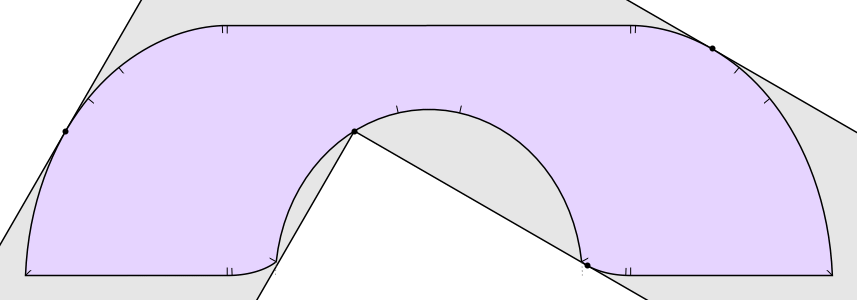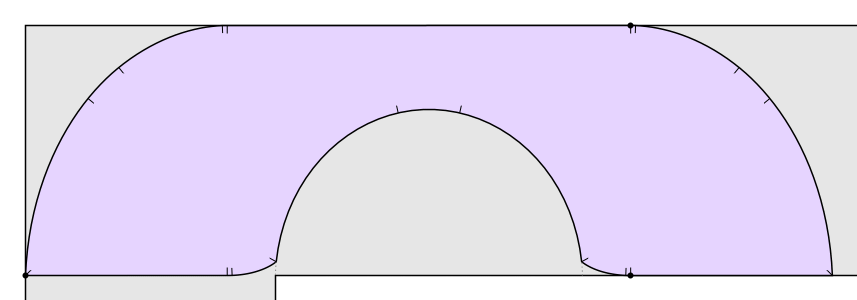
This question was first published by Leo Moser in 1966. The animation above, made by Claudio Rocchini, shows one attempt to solve this problem. It’s called the Hammersley sofa, since it was discovered by John Michael Hammersley in 1968. Its area has this charming value:

$$ \frac{\pi}{2} + \frac{2}{\pi} = 2.2074 \dots $$

But it’s not the best known solution! In 1992, Joseph Gerver found a shape of area

$$ 2.219531668871 \dots $$

that fits around the bend in the hallway. Basically Gerver rounded off some of the corners of Hammersley’s sofa. The resulting shape has a boundary consisting of 3 straight line segments and 15 curved segments, each described by an analytic expression:

On the other hand, Hammersley showed that any solution has to have area at most

$$ 2 \sqrt{2} = 2.8282 \dots $$

So, the moving sofa problem remains unsolved. However, Philip Gibbs recently used a numerical method to solve a discretized version of this problem, and he obtained a sofa whose area agrees with Gerver’s to about 8 significant figures:

• Philip Gibbs, A computational study of sofas and cars, 13 November 2014.

So, it seems reasonable to conjecture that Gerver’s solution is optimal!

For more, see:

• Moving sofa problem, Wikipedia.

• Neal R. Wagner, The sofa problem, American Mathematical Monthly 83 (1976), 188–189.

• Moving sofa problem, Wolfram Mathworld.

• Steven Finch Moving sofa constant, MathSoft Constants.

The last two pages explain Gerver’s sofa and compute its area. Gerver’s original paper is here:

• Joseph L. Gerver, On moving a sofa around a corner, Geometriae Dedicata 42 (1992), 267–283.

while Hammersley’s proposed solution appeared in this tendentiously titled article:

• John Michael Hammersley, On the enfeeblement of mathematical skills by modern mathematics and by similar soft intellectual trash in schools and universities, Bull. Inst. Math. App. 4 (1968), 66–85.

Dan Romik has an interesting paper on the sofa problem, and a variant that demands the sofa be symmetrical and optimal for negotiating both right and left turns in a hallway:

• Dan Romik, Differential equations and exact solutions in the sofa problem, 2016.

He also has a nice webpage featuring movies of several sofas, including the Gerver sofa shown above:

• Dan Romik, The moving sofa problem.

Claudio Rocchini, who created the animated gif above, put it on Wikimedia Commons with a Creative Commons Attribution-Share Alike 3.0 Unported license.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!