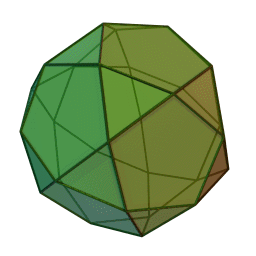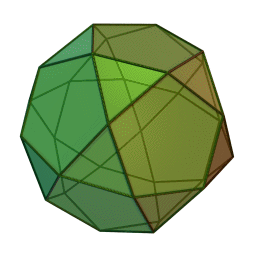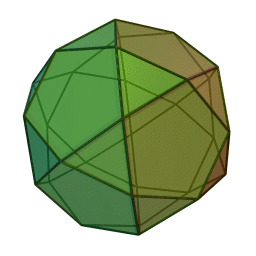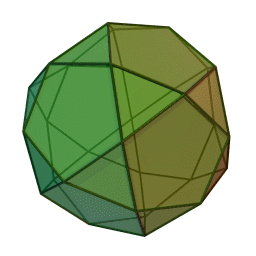
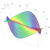
The icosidodecahedron can be built by truncating either a regular icosahedron or a regular dodecahedron. It has 30 vertices, one at the center of each edge of the icosahedron—or equivalently, one at the center of each edge of the dodecahedron. It is a beautiful, highly symmetrical shape:
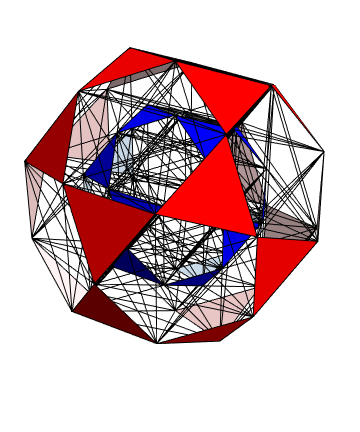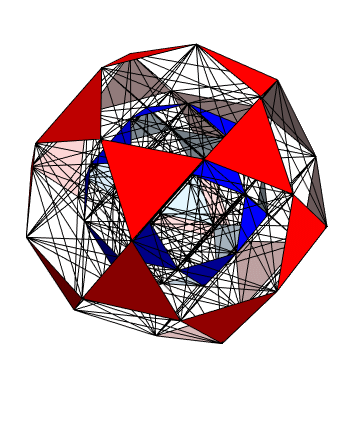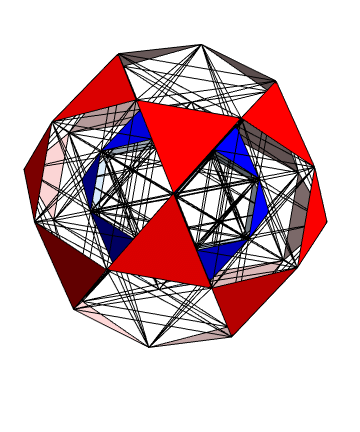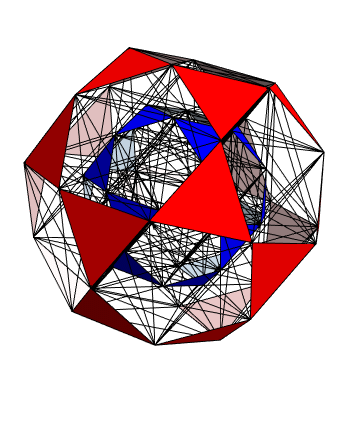
But the icosidodecahedron is just a shadow of an even more symmetrical shape with twice as many vertices in twice as many dimensions! Namely, it’s a projection down to 3d space of the D6 root polytope, a 6-dimensional convex polytope with 60 vertices. You can see all 60 vertices in the movie above, which was made by Greg Egan. They lie on two icosidodecahedra, one larger than the other.
To understand this construction in context, it is helpful to start with the group consisting of rotational symmetries of the icosahedron, or dodecahedron. This group has 60 elements, so its ‘double cover’ consists of 120 unit quaternions.
These 120 unit quaternions are the vertices of a regular polytope in 4 dimensions called the 600-cell, since it has 600 tetrahedral faces. With suitable coordinates, the coordinates of all these vertices lie in what Conway and Sloane call the golden field:
Q[√5]={x+y√5:x,y∈Q}
Namely, we can take the 600-cell’s vertices to be
±1,±1±i±j±k2,±i±ϕj±Φk2
together with everything obtained from these by even permutations of the quaternions 1,i,j,k, where
Φ=√5+12=1.6180339…
and
ϕ=√5–12=0.6180339…
are the ‘big’ and ‘little’ golden ratios.
Since these 120 quaternions form a group under quaternion multiplication, their integer linear combinations form a subring of the quaternions, which Conway and Sloane call the icosians.
Any icosian is of the form
a+bi+cj+dk
where the numbers a,b,c,d live in the golden field. Since each of these numbers is of the form x+y√5 with x,y rational, we can think of an icosian as an 8-tuple of rational numbers. However, we don’t get all 8-tuples, but only those lying in a certain lattice.
There is a way to think of this as the E8 lattice. To do this, Conway and Sloane put a new norm on the icosians as follows. There is usual quaternionic norm
‖a+bi+cj+dk‖2=a2+b2+c2+d2
But for an icosian this is always of the form x+√5y for some rationals x and y. So, Conway and Sloane define a new norm on the icosians by setting
|a+bi+cj+dk|2=x+y
With this norm, the icosians form a copy of the E8 lattice.
The 240 shortest nonzero vectors in this lattice, called the roots of E8, are the vertices of an 8-dimensional convex polytope sometimes called the E8 root polytope. However, if we remember that each of these 240 vectors came from a quaternion, we also get 240 special quaternions. These turn out to be the vertices of two 600-cells in the quaternions. In the usual quaternionic norm, one of these 600-cells is larger than the other by a factor of Φ.
In fact, there is an orthogonal projection from R8 down to R4 that maps the E8 root polytope to the 600-cell! So, in a very real sense, the 600-cell is the ‘shadow’ of a polytope with twice as many vertices, living in a space whose dimension is twice as large.
This relationship is mirrored by relationship between the icosidodecahedron and the D6 root polytope. The icosidodecahedron is a ‘shadow’ of the D6 root polytope, which has twice as many vertices as the icosidodecahedron, and lives in a space whose dimension is twice as large.
Let’s see how this works!
A pure imaginary icosian is one of the form
ai+bj+ck
for real a,b,c. In fact a,b and c will necesssarily lie in the golden field, so we can think of a pure imaginary icosian as a 6-tuple of rational numbers. We don’t get all 6-tuples this way, but only those lying in a certain lattice.
We can think of this as the D6 lattice using the method of Conway and Sloane. We have
‖ai+bj+ck‖2=a2+b2+c2
For a pure imaginary icosian this is always of the form x+√5y for some rationals x and y. So, we can define a new norm on the pure imaginary icosians by
|ai+bj+ck|2=x+y
Then the pure imaginary icosians form a copy of the D6 lattice.
In this way the 60 shortest nonzero vectors in the D6 lattice—the so-called roots of D6— correspond to two copies of the 30 vertices of the icosidodecahedron. In fact, there is an orthogonal projection from 6-dimensional Euclidean space down to 3-dimensional Euclidean space such that the icosidodecahedron is the image of the D6 root polytope. This is shown in Greg Egan’s image above.
In a bit more detail: the usual coordinatization of the D6 root lattice is
D6={(x1,…,x6):xi∈Z,6∑i=1xiiseven}
The D6 roots are:
(±1,±1,0,0,0,0)
and all vectors obtained by permuting the six coordinates. These roots are sent to the vertices of an icosidodecahedron by the linear map
T:R6→R3
given as a 3×6 matrix by
(ΦΦ−1−10000Φ−Φ−11−1100ΦΦ)
The rows of this matrix are orthogonal, all with the same norm, so after rescaling it by a constant factor T:R6→R3 becomes an orthogonal projection. The columns of this matrix are six vertices of an icosahedron, chosen so that we never have a vertex and its opposite. Thus, for any pair of columns, they are either neighboring vertices of the icosahedron, or a vertex and the opposite of a neighboring vertex.
The map T will thus map any D6 root to either the sum or the difference of two neighboring icosahedron vertices. In this way we obtain all possible sums and differences of neighboring vertices of the icosahedron. The sums give 30 vectors that are vertices of the larger icosidodecahedron shown in red above. The differences give 30 vectors of the smaller icosidodecahedron shown in blue.
It is easy to see that the sums of neighboring vertices of the icosahedron give the vertices of a icosidodecahedron, since by definition, the icosidodecahedron has vertices at the midpoints of the edges of the icosahedron. It is less obvious that the differences of neighboring vertices of the icosahedron give the vertices of a second, smaller icosidodecahedron. In fact, the vectors defining the vertices of the larger icosidodecahedron turn out to be precisely Φ times the vectors defining the vertices of the smaller one.
The 3 × 6 matrix above can be extended to a 4 × 8 matrix that does the same job for the E8 root polytope and the 600-cell:
(Φ+1Φ−100000000ΦΦ−1−1000000Φ−Φ−1100−1100ΦΦ)
After rescaling by a suitable constant, this gives an orthogonal projection from R8 to R4 that maps the usual E8 roots
{x∈R8:allxi∈Zorallxi∈Z+12,∑ixiiseven,x⋅x=2}
to the vertices of two 600-cells, one larger than another by a factor of Φ. Thus, this projection maps the E8 root polytope to a 600-cell.
For the larger context of this work, see:
• Andreas Fring and Christian Korff, Non-crystallographic reduction of Calogero-Moser models, Jour. Phys. A 39 (2006), 1115–1131.
• Pierre-Philippe Dechant, Celine Boehm and Reidun Twarock, Affine extensions of non-crystallographic Coxeter groups induced by projection.
• J. Gregory Moxness, The 3d visualization of E8 using an H4 folding matrix, math version.
The relevant portion of the first paper is summarized here:
• John Baez, This Week’s Finds in Mathematical Physics (Week 270).
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!


Polihedrones are most exciting subject to study in mathematics in my opinion.