Pentagon-Decagon Packing

/ 1 February, 2015
Pentagon-Decagon Packing - Greg Egan

Pentagon-Decagon Packing – Greg Egan

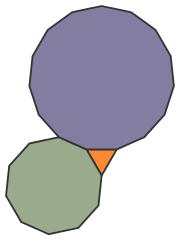
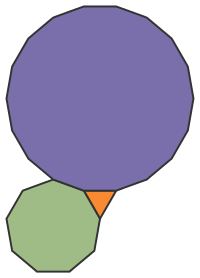
Two regular pentagons and a regular decagon meet snugly at a vertex: their interior angles sum to 360°. However, they can’t tile the plane. However, they come fairly close, as shown in this picture by Greg Egan.

Say we have three regular polygons with \(p, q,\) and \(r\) sides, respectively. Their interior angles will sum to 360° if and only if

$$ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} $$

So, two regular pentagons and a regular decagon can meet snugly at a vertex because

$$ \frac{1}{5} + \frac{1}{5} + \frac{1}{10} = \frac{1}{2} $$

In fact there are 10 solutions of the equation

$$ \frac{1}{p} + \frac{1}{q} + \frac{1}{r} = \frac{1}{2} $$

for natural numbers \(p, q, \) and \(r\), not counting the order. Of these, only 4 give tilings of the plane by regular polygons. The other 6 are ‘forbidden’.

Here are all 10 solutions:

  1. $$ \frac{1}{6} + \frac{1}{6} + \frac{1}{6} = \frac{1}{2} $$
    gives the regular hexagonal tiling.

  2. $$ \frac{1}{5} + \frac{1}{5} + \frac{1}{10} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives the packing shown above, and three more described by Robert Fathauer.

    Regular Polygons Meeting at Vertex: 5.5.10

  3. $$ \frac{1}{4} + \frac{1}{8} + \frac{1}{8} = \frac{1}{2} $$
    gives the semiregular truncated square tiling.

  4. $$ \frac{1}{4} + \frac{1}{6} + \frac{1}{12} = \frac{1}{2} $$
    gives the semiregular truncated trihexagonal tiling.

  5. $$ \frac{1}{4} + \frac{1}{5} + \frac{1}{20} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives a packing described by Robert Fathauer.

    Regular Polygons Meeting at Vertex: 4.5.20

  6. $$ \frac{1}{3} + \frac{1}{12} + \frac{1}{12} = \frac{1}{2} $$
    gives the semiregular truncated hexagonal tiling.

  7. $$ \frac{1}{3} + \frac{1}{10} + \frac{1}{15} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives two packings described by Robert Fathauer and Kevin Jardine.

    Regular Polygons Meeting at Vertex: 3.10.15

  8. $$ \frac{1}{3} + \frac{1}{9} + \frac{1}{18} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives a packing described by Robert Fathauer.

    Regular Polygons Meeting at Vertex: 3.9.18

  9. $$ \frac{1}{3} + \frac{1}{8} + \frac{1}{24} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives two packings discovered by Robert Fathauer and Kevin Jardine.

    Regular Polygons Meeting at Vertex: 3.8.24

  10. $$ \frac{1}{3} + \frac{1}{7} + \frac{1}{42} = \frac{1}{2} $$
    does not give a tiling by regular polygons, but it gives a packing discovered by Robert Fathauer.

    Regular Polygons Meeting at Vertex: 3.7.42

Because 42 is the largest number appearing in the above list of solutions, this number—or twice this number—appears in Hurwitz’s automorphism theorem. This says that the number of orientation-preserving conformal transformations of a compact Riemann surface of genus \(g > 1\) is at most \(84(g − 1)\). For more on this, see:

• John Baez, 42.

For more on the 6 ‘forbidden tilings’—the 6 solutions on the list above that do not give tilings of the plane by regular polygons—see this set of webpages:

• Kevin Jardine, Imperfect congruence: Kepler, Dürer and the mystery of the forbidden tilings.

Also see:

• Tiling by regular polygons, Wikipedia.

The above pictures of the 6 forbidden tilings were created by dllu and placed on Wikimedia Commons under a Creative Commons CC0 1.0 Universal Public Domain Dedication copyright.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

Related posts