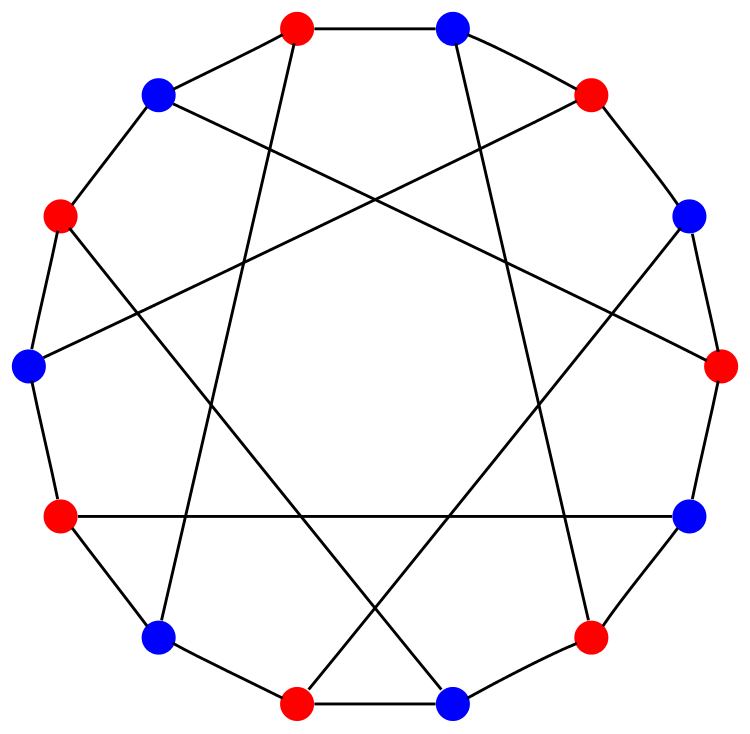
This is the Heawood graph. This graph can be drawn on a torus with no edges crossing in such a way that it divides the torus into 7 hexagons, each pair of which shares an edge:
In 1890, Percy John Heawood proved that for any map drawn on a torus, it takes at most 7 colors to ensure that no two countries sharing a common boundary have the same color. The Heawood graph proves that the number 7 is optimal.
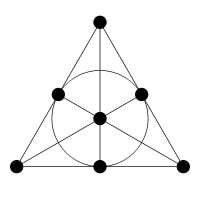
One nice way to construct the Heawood graph starts with the Fano plane, the projective plane over the field F2. The Fano plane has 7 point and 7 lines:
The red vertices in the top picture of the Heawood graph correspond to the 7 points of the Fano plane, while the blue vertices correspond to the 7 lines. An edge connects a red vertex to a blue vertex iff the corresponding point lies on the corresponding line. So, we say the Heawood graph is the Levi graph of the Fano plane.
Since there are 7 points and 7 lines in the Fano plane, the Heawood graph has 14 vertices. Since each point in the Fano plane lies on 3 lines, the Heawood graph has 21 edges.
The Fano plane has symmetry group PGL(3,F2), a group with 168 elements. This group therefore also acts as symmetries of the Heawood graph. These symmetries send red vertices to red vertices and blue vertices to blue ones. However, the Heawood graph also has symmetries that switch red and blue vertices. These arise from the fact that the Fano plane is self-dual: if we call points ‘lines’ and lines ‘points’, the resulting structure is again a copy of the Fano plane.
The symmetry group of the Heawood graph has 336 elements, since half of the symmetries preserve the color of the vertices while the other half switch colors. In fact, this group is the automorphism group Aut(PGL(3,F2)).
To see this, first note that Aut(PGL(3,F2)) contains PGL(3,F2), which acts as inner automorphisms. It also contains transposition
g↦g⊤
which is an outer automorphism of order 2. Together with the 168 inner automorphisms, transposition generates Aut(PGL(3,F2)), which is a group of order 336. The inner automorphisms map the stabilizer of any point in the Fano plane to the stabilizer of another point, and map the stabilizer of any line to the stabilizer of another line. The outer automorphisms map the stabilizer of a point to the stabilizer of a line, and vice versa.
In fact, we have
PGL(3,F2)≅PSL(2,F7)
and
Aut(PGL(3,F2))≅PGL(2,F7)
so we can also understand the symmetries of the Fano plane and the Heawood graph in terms of PSL(2,F7) and PGL(2,F7), which act as symmetries of the projective line over the field with 7 elements, F7.
The Heawood graph is also a (3,6)-graph, meaning that every vertex has 3 neighbors and every cycle has length at least 6. It has the least possible number of vertices for a (3,6)-graph, so it is called a (3,6)-cage. It is, in fact, the unique (3,6)-cage.
There are 28 cycles of length 6 in the Heawood graph. These correspond to the 28 triangles in the Fano plane.
For more, see:
• Heawood graph, Wikipedia.
• PSL(2,7), Wikipedia.
• Projective general linear group: PGL(2,7), Groupprops.
• Cage graph, Wolfram Mathworld.
The featured picture of the Heawood graph was drawn by Koko90, who placed it on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license. David Eppstein drew the Heawood graph on a torus, put it on Wikicommons, and released it into the public domain. A German Wikicommons user named Gunther drew the picture of the Fano plane, put it on Wikicommons, and released it into the public domain.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!

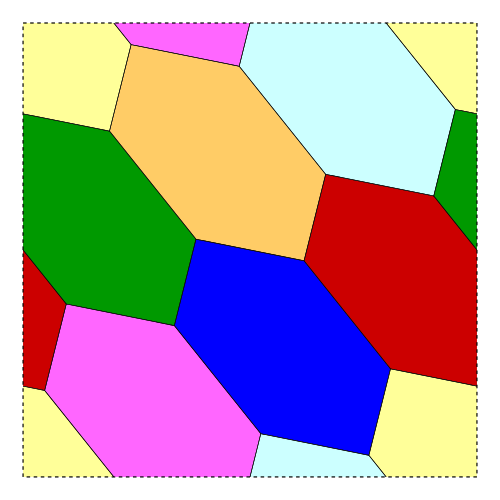



Beautiful stuff. So you get a lovely tessellation of the flat torus.
This made me wonder if you can get a toroidal polyhedron with 7 hexagonal faces, each sharing an edge with the other 6. Google informs me about the Szilassi polyhedron, which has 3 pairs of congruent non-convex hexagons and one convex hexagon. In some sense, it’s an analog of the tetrahedron which shows that you need 4 colors for the sphere, although of course the tetrahedron is rather more symmetric.
Cool! And the dual of the Czilassi polyhedron is the Csaszar polyhedron!