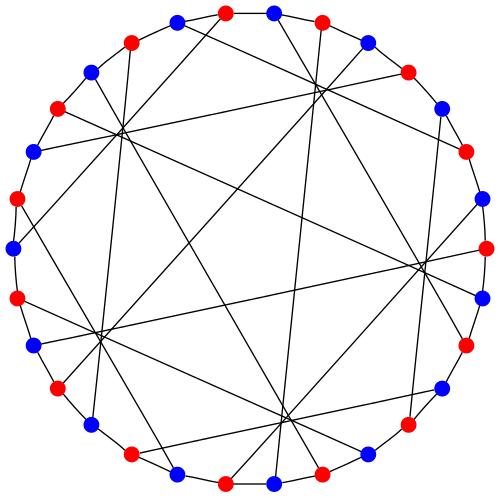
This picture shows the Tutte–Coxeter graph. This graph was discovered by the famous graph theorist William Thomas Tutte in 1947, but its remarkable properties were studied further by him and the geometer H. S. M. Coxeter in a pair of papers published in 1958.

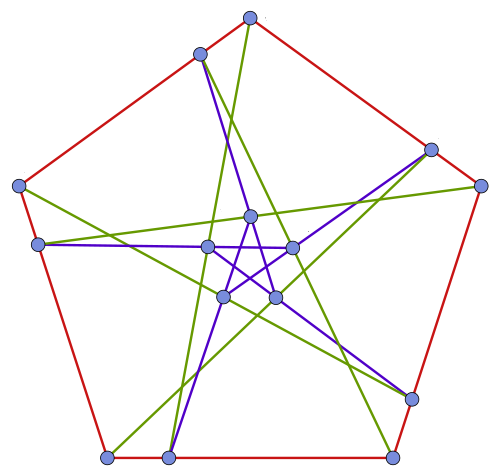
One way to construct this graph starts with the Cremona–Richmond configuration. This is a configuration of 15 points and 15 lines, with 3 points on each line and 3 lines through each point, and containing no triangles:

The red vertices in the Tutte–Coxeter graph correspond to the 15 points of the Cremona–Richmond configuration, while the blue vertices correspond to the 15 lines. An edge connects a red vertex to a blue vertex iff the corresponding point lies on the corresponding line. So, we say the Tutte–Coxeter graph graph is the Levi graph of the Cremona–Richmond configuration.

Since there are 15 points and 15 lines in the Cremona–Richmond configuration, the Tutte–Coxeter graph has 30 vertices. Since each point in the Cremona–Richmond configuration lies on 3 lines, the Tutte–Coxeter graph has 45 edges.

The Cremona–Richmond configuration, in turn, is best understood in terms of special features of $\mathrm{S}_6$, the only symmetric group to possess an outer automorphism.

Let \(S = \{1,2,3,4,5,6\}\). Of course the symmetric group \(S_6\) acts on \(S\), but James Sylvester found a different action of \(S_6\) on a 6-element set, which in turn gives an outer automorphism of \(S_6\).

To do this, he made the following definitions:

• A duad is a 2-element subset of \(S\). Note that there are \( {6 \choose 2} = 15 \) duads.

• A syntheme is a set of 3 duads forming a partition of \(S\). There are also 15 synthemes.

• A synthematic total is a set of 5 synthemes partitioning the set of 15 duads. There are 6 synthematic totals.

Any permutation of \(S\) gives a permutation of the set \(T\) of synthematic totals, so we obtain an action of \(S_6\) on \(T\). Choosing any bijection betweeen \(S\) and \(T\), this in turn gives an action of \(S_6\) on \(S\), and thus a homomorphism from \(S_6\) to itself. Sylvester showed that this is an outer automorphism.

We can interpret all this combinatorics in terms of the Cremona–Richmond configuration. The points of the Cremona–Richmond configuration are the 15 duads. Similarly, the lines of this configuration are the 15 synthemes. We say that a point lies on a line iff the corresponding duad lies in the corresponding syntheme.

Since the square of the outer automorphism of \(S_6\) is the identity, switching points and lines in the Cremona–Richardson configuration gives another Cremona–Richardson configuration.

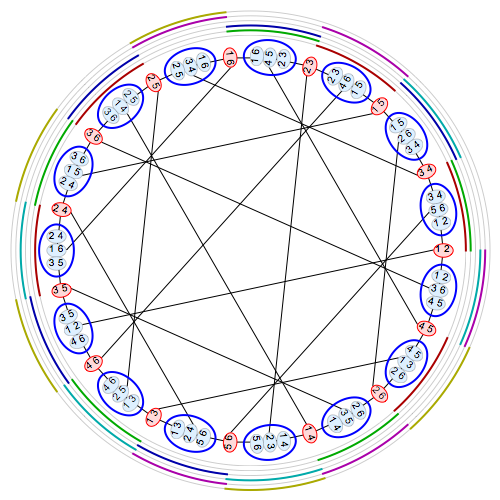
We can also interpret this combinatorics directly in terms of the Tutte–Coxeter graph. Greg Egan has drawn a version of the Tutte–Coxeter graph with duads and synthemes:

Here the 15 red vertices of the Tutte–Coxeter graph are drawn as duads, while the 15 blue vertices are drawn as synthemes. We draw an edge from a duad to a syntheme whenever the duad lies in the syntheme. You can see that there are 3 duads in each sytheme, and each duad lies in 3 synthemes.

The 6 concentric rings around the picture are the 6 synthematic totals. A band of color appears in one of these rings near some syntheme if that syntheme is part of that synthematic total.

The outer automorphisms of \(S_6\) give symmetries of the Tutte–Coxeter graph that switch the red and blue vertices. The inner automorphisms, which correspond to elements of \(S_6\), also give symmetries: for each element of \(S_6\), the Tutte–Coxeter graph has a symmetry that permutes the numbers in the picture.

The group \(\mathrm{Aut}(S_6)\) has

$$ 2 \times 6! = 1440 $$

elements, coming from the \(6!\) inner automorphisms of \(S_6\) and a chosen outer automorphism of order 2. In fact, \(\mathrm{Aut}(S_6)\) is the whole symmetry group of the Tutte–Coxeter graph.

How do the outer automorphisms of \(S_6\) give symmetries of the Tutte–Coxeter graph that switches the red and blue vertices? There are various ways to see this. Greg Egan gave one, which focuses on the reverse question: how do symmetries of the Tutte–Coxeter graph give automorphism of \(S_6\)?

Let \(\mathrm{Symm}(TC)\) be the complete symmetry group of the Tutte–Coxeter graph. We’ll construct a homomorphism

$$ \psi \colon \mathrm{Symm}(TC) \to \mathrm{Aut}(S_6) $$

and sketch out why it’s an isomorphism.

We know there’s an isomorphism between \(S_6\) and the subgroup of the symmetries of the Tutte-Coxeter graph that preserve the duad/syntheme distinction. We’ll call this

$$ \phi \colon S_6 \to \mathrm{Symm}_0(TC), $$

where \(\mathrm{Symm}_0(TC)\) is the subgroup where duads and synthemes don’t mix.

Suppose \(g\) is any element of \(\mathrm{Symm}(TC)\), and we want to obtain an automorphism of \(S_6\), \( \psi (g) \colon S_6 \to S_6 \). For any permutation \(p \in S_6\), we define:

$$ \psi(g)(p) = \phi^{-1}(g \phi(p) g^{-1}) $$

So we act with the inverse of our graph symmetry \(g\), then act with the graph symmetry corresponding to the permutation \(p\), then act with the graph symmetry \(g\)… and then turn the resulting overall graph symmetry into an element of \(S_6\).

This is well-defined for any \(g\) in \(\mathrm{Symm}(TC)\), even if \(g\) swaps duads and synthemes, because we use both \(g\) and \(g^{-1}\), and \(\phi(p)\) preserves the duad/syntheme distinction, so the product:

$$ g \phi(p) g^{-1} $$

will be in \(\mathrm{Symm}_0(TC)\).

It is easy to check that any inner automorphism of \(S_6\) is in the range of \(\psi\). I checked that outer automorphisms are in the range too, by explicitly turning a reflection symmetry of the graph that swaps duads and synthemes into an automorphism of \(S_6\). It wasn’t an inner automorphism. Thus, \(\psi\) is onto. To check that it’s one-to-one, the main step is to note that it’s one-to-one on \(\mathrm{Symm}_0(TC)\), because this group, isomorphic to \(S_6\), has trivial center.

Another method, more complicated but appealing in some ways, follows ideas borrowed from Klein’s Erlangen Program. The idea here is to build geometries starting from groups. If a group \(G\) acts on some geometrical structure, any ‘figure’ in this structure will be stabilized by some subgroup of \(G\). We can turn this around by defining ‘figures’ to be subgroups of \(H\).

We can use this idea to define the Tutte–Coxeter graph in a way that makes it obviously have $\mathrm{Aut}(S_6)$ as symmetries. Let \(G\) be a group abstractly isomorphic to \(S_6\), but let’s not think of it as a group of permutations of a 6-element set, since the whole point is that we can do this in two inequivalent ways, related by an outer automorphism, and we don’t want to break the automorphism symmetry by favoring either way.

One can look up in a table that \(G\) has 30 subgroups isomorphic to \(S_4 \times S_2\). These will be the vertices of our graph.

Given two such subgroups, \(H\) and \(H’\), we draw an edge between the corresponding vertices iff \(H \cap H’\) is isomorphic to \(D_4 \times S_2\), where \(D_4\) is the 8-element dihedral group that acts as symmetries of a square.

Since we built it from \(G\), the resulting graph is obviously acted on by \(\mathrm{Aut}(G) \cong \mathrm{Aut}(S_6).\). What is not obvious is that it is the Tutte–Coxeter graph! For this we need some more facts about subgroups of \(S_6\).

The 30 subgroups of \(G\) isomorphic to \(S_4 \times S_2\) come in two classes: 15 are conjugate to each other, and the other 15 are conjugate to each other. If we identify \(G\) with a group of permutations of a 6-element set, 15 of these subgroups are stabilizers of duads, while the other 15 are stabilizers of synthemes.

However, which is which? That depends on how you identify $G$ with a group of permutations of a 6-element set! Here we are deliberately not making that decision.

But suppose we do. If \(H\) is the stabilizer of a duad, and \(H’\) is the stabilizer of a syntheme, and the duad lies in the syntheme, then \(H \cap H’\) will be isomorphic to \(D_4 \times S_2\). In other cases, \(H \cap H’\) will not be isomorphic to \(D_4 \times S_2\). So, our construction gives the Tutte–Coxeter graph.

In fact, \(G\) has exactly 45 subgroups isomorphic to \(D_4 \times S_2\) so we can identify the edges of our graph with these subgroups.

For the necessary facts about subgroups of \(S_6\), see:

• Götz Pfeiffer, Subgroups.

On a different note, it is worth noting an analogy between the Tutte–Coxeter graph and a graph we discussed earlier:

• Heawood graph.

Just as the Heawood graph is the Levi graph of the Fano plane, the Tutte–Coxeter graph is the Levi graph of the Cremona–Richardson configuration. Just as \(\mathrm{PGL}(3,\mathbb{F}_2)\) acts as symmetries of the Fano plane, \(S_6\) acts as symmetries of the Cremona–Richardson configuration. Just as \(\mathrm{PGL}(3,\mathbb{F}_2)\) has an outer automorphism of order 2, so does the \(S_6\). Just as \(\mathrm{Aut}(\mathrm{PGL}(3,\mathbb{F}_2))\) is a group containing \(\mathrm{PGL}(3,\mathbb{F}_2)\) as a subgroup of index 2, so \(\mathrm{Aut}(S_6)\) is a group containing \(S_6\) as a subgroup of index 2. Just as \(\mathrm{Aut}(\mathrm{PGL}(3,\mathbb{F}_2))\) is the symmetry group of the Heawood graph, so \(\mathrm{Aut}(S_6)\) is the symmetry group of the Tutte–Coxeter graph. Just as the Heawood graph gets a 2-coloring from the fact that its vertices correspond to points and lines in the Fano plane, the Tutte–Coxeter graph gets a 2-coloring from the fact that its vertices correspond to points and lines in the Cremona–Richardson configuration. And just as \(\mathrm{PGL}(3,\mathbb{F}_2)\) is the group of symmetries of the Heawood graph preserving this 2-coloring, so \(S_6\) is the group of symmetries of the Tutte–Coxeter graph preserving this 2-coloring.

We have seen that the Heawoof graph is a (3,6)-cage. Similarly, the Tutte–Coxeter graph is a (3,8)-cage.

Recall what this means. First, the Tutte–Coxeter graph is a (3,8)-graph, meaning that every vertex has 3 neighbors and every cycle has length at least 8. Second, it has the smallest possible number of vertices for a (3,8)-graph, so it is called a (3,8)-cage. It is, in fact, the unique (3,8)-cage.

Puzzle 1: How many cycles of length 8 does the Tutte–Coxeter graph contain?

Puzzle 2: What do these cycles correspond to in the Cremona–Richmond configuration?

Puzzle 3: What do these cycles correspond to in terms of duads, synthemes or other features of the 6-element set?

For more, see:

• Tutte–Coxeter graph, Wikipedia.

• Cremona–Richardon configuration, Wikipedia.

• Peter Cameron, The symmetric group, 3, Peter Cameron’s Blog.

The Cremona–Richmond configuration is an example of a generalized quadrangle, and it is sometimes called \(\mathrm{GQ}(2,2)\). Richard Green discusses it under that name here:

• Richard Green, The generalized quadrangle GQ(2,2).

For some of the category-theoretic ramifications of the outer automorphism of \(S_6\), see:

• John Baez, A wrinkle in the mathematical universe, The n-Category Café.

The featured picture of the Tutte–Coxeter graph was made by Koko90 and placed on Wikicommons under a Creative Commons Attribution-Share Alike 3.0 Unported license. The picture of the Cremona–Richmond configuration was made by David Eppstein, put into the public domain on Wikicommons, and then modified by John Baez. The picture of the Tutte–Coxeter graph with duads and synthemes was made by Greg Egan.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!