Dyck Words – Tilman Piesk
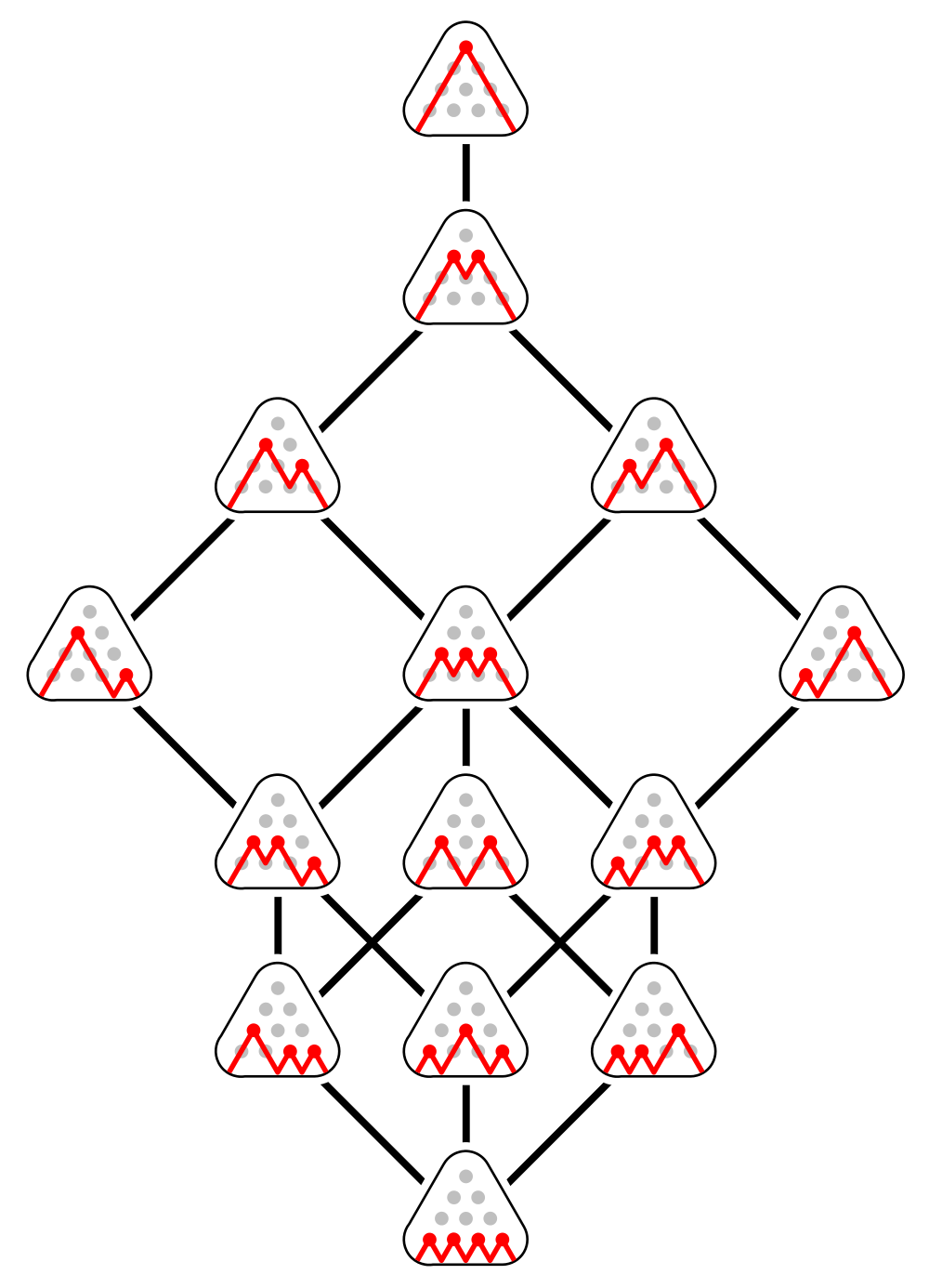
This picture by Tilman Piesk shows the 14 Dyck words of length 8. A Dyck word is a balanced string of left and right parentheses, like these:
$$ (((()))) $$
$$ ((()())) $$
$$ ((())()) \qquad (()(())) $$
$$ ((()))() \qquad (()()()) \qquad ()((())) $$
$$ (()())() \qquad (())(()) \qquad ()(()()) $$
$$ (())()() \qquad ()(())() \qquad ()()(()) $$
$$ ()()()() $$
These are, in fact, all 14 Dyck words of length 8.
The condition of being balanced says that as we read a Dyck word from left to right there is at each stage at least as many left parentheses as right ones, with an equal number by the time we reach the end. In the picture, a left parenthesis is shown as upward-slanting line segment, and a right parenthesis as a downward-slanting one. The condition of being balanced then translates into the fact that the resulting ‘mountain range’ starts and ends at ground level, and never goes below ground.
The picture uses this way of drawing to illustrate a certain partial order on the set of Dyck words: \(w \le w’\) iff the mountain range corresponding to \(w’\) is at least as high at all points as the mountain range corresponding to \(w\). This partial order makes the set of Dyck words into a lattice: any two Dyck words have a least upper bound and greatest lower bound.
Puzzle 1: Is it true that whenever \(w \le w’\) we can go from \(w\) to \(w’\) by repeated applications of this rewrite rule:
\[ )( \rightarrow () \; ? \]
The set of all Dyck words is called the Dyck language. This plays a fundamental role in the study of expressions that involve parentheses. We can define Dyck languages with more than one kind of parentheses; for example,
$$ ([])(([])[])) $$
is a Dyck word on two kinds of parentheses. The Chomsky–-Schützenberger representation theorem characterizes context-free languages in terms of the Dyck language on two parentheses.
Returning to the Dyck language with just one kind of parenthesis, the number of Dyck words of length \(2n\) is the \(n\)th Catalan number.
The Catalan numbers count many different things. So, there are a number of different interesting partial orders on sets that are in natural one-to-one correspondence with the set of Dyck words of length \(2n\). For example, the set \(X_n\) consisting of expressions built from \(n+1\) letters using a nonassociative binary product is in natural bijection with the set of Dyck words of length \(n\). The Tamari lattice is the set \(X_n\) ordered in such a way that \(w \ge w’\) iff \(w\) is obtained from \(w’\) by repeated applications of this rewrite rule:
\[ (xy)z \to x(yz). \]
Here \(x,y,z\) are expressions built from letters, not necessarily single letters, and the rewrite rule can be used anywhere in a larger expression. For example, we have
\[ (((ab)c)d)e \to ((ab)(cd))e .\]
Below is a picture of the Tamari lattice \(X_4\), where applications of the rewrite rule are drawn as edges going up:
Tamari Lattice – David Eppstein
Like the lattice at the top of this page, \(X_4\) has 14 elements. However, they are nonisomorphic as lattices. There is an \(n-1\)-dimensional polytope, the associahedron, whose vertices are the elements of \(X_n\) and whose edges are applications of the rewrite rule \((xy)z \to x(yz)\). The picture above shows the 3-dimensional associahedron.
Puzzle 2: Describe a bijection between the set of Dyck words of length \(2n\) and the set \(X_n\).
Puzzle 3: You can use your bijection and the partial order on Dyck words described earlier to put a partial order on \(X_n\). Describe this partial order explicitly.
For a review of various partial orders on the set of Dyck words, with references, see:
• J. L. Baril, J. M. Pallo, The phagocyte lattice of Dyck words, Order 23 (2006), 97–107.
Tilman Piesk put the top picture on Wikicommons with a Creative Commons Attribution 3.0 Unported license. David Eppstein put his picture into the public domain on Wikicommons.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!
