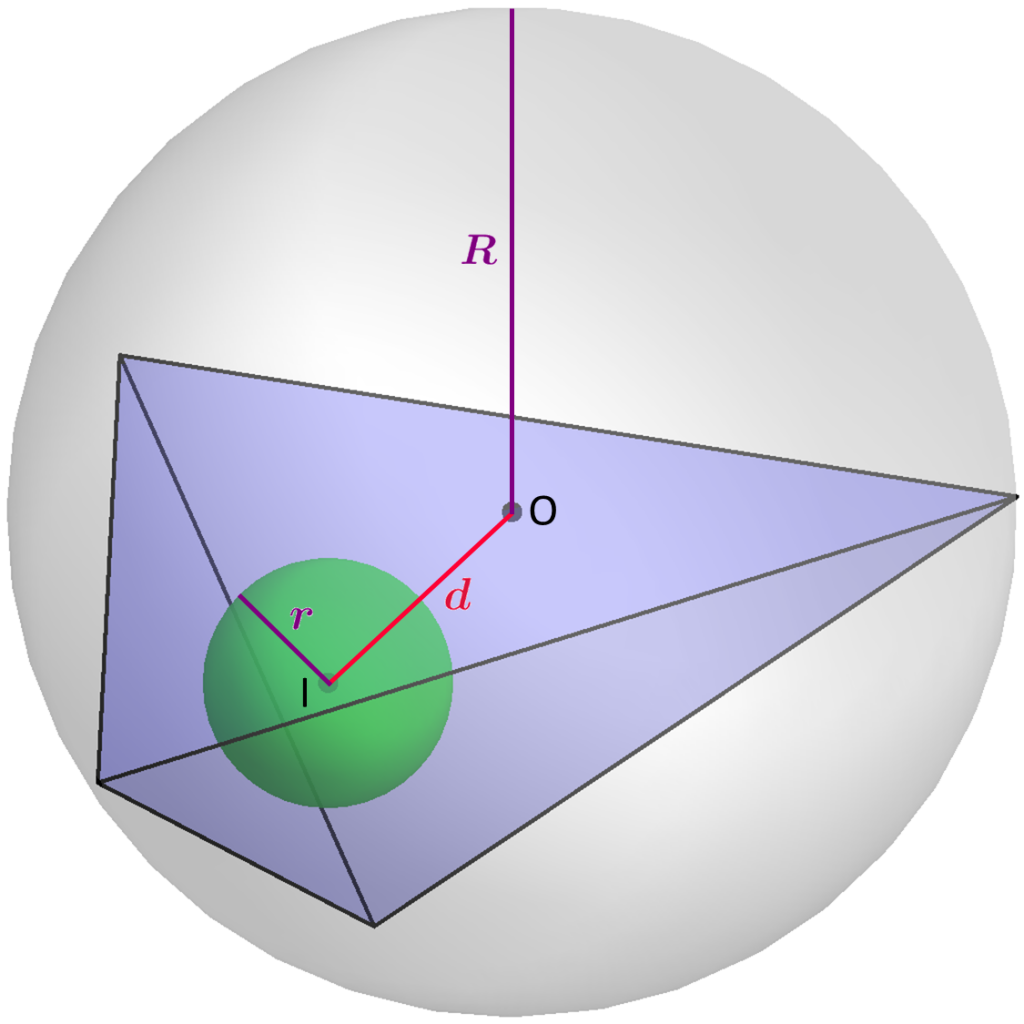
When can you fit a tetrahedron between two nested spheres?
Here’s the answer. Suppose the radius of the large sphere is R and the radius of the small one is r. Suppose the distance between their centers is d. Then you can fit a tetrahedron between these spheres if and only if the Grace–Danielsson inequality holds:
d2≤(R+r)(R–3r)
This was independently proved by Grace in 1917 and Danielsson in 1949. But Antony Milne has found a new proof of this inequality using quantum information theory:
• Antony Milne, The Euler and Grace-Danielsson inequalities for nested triangles and tetrahedra: a derivation and generalisation using quantum information theory.
The rough idea is this. Suppose Alice and Bob have entangled qubits. By choosing which measurements to perform, Bob can ‘steer’ the results of Alice’s measurements. Given all possible measurements by Bob, the set of results Alice can get forms an ellipsoid… and studying this ellipsoid leads to the Grace–Danielsson inequality.
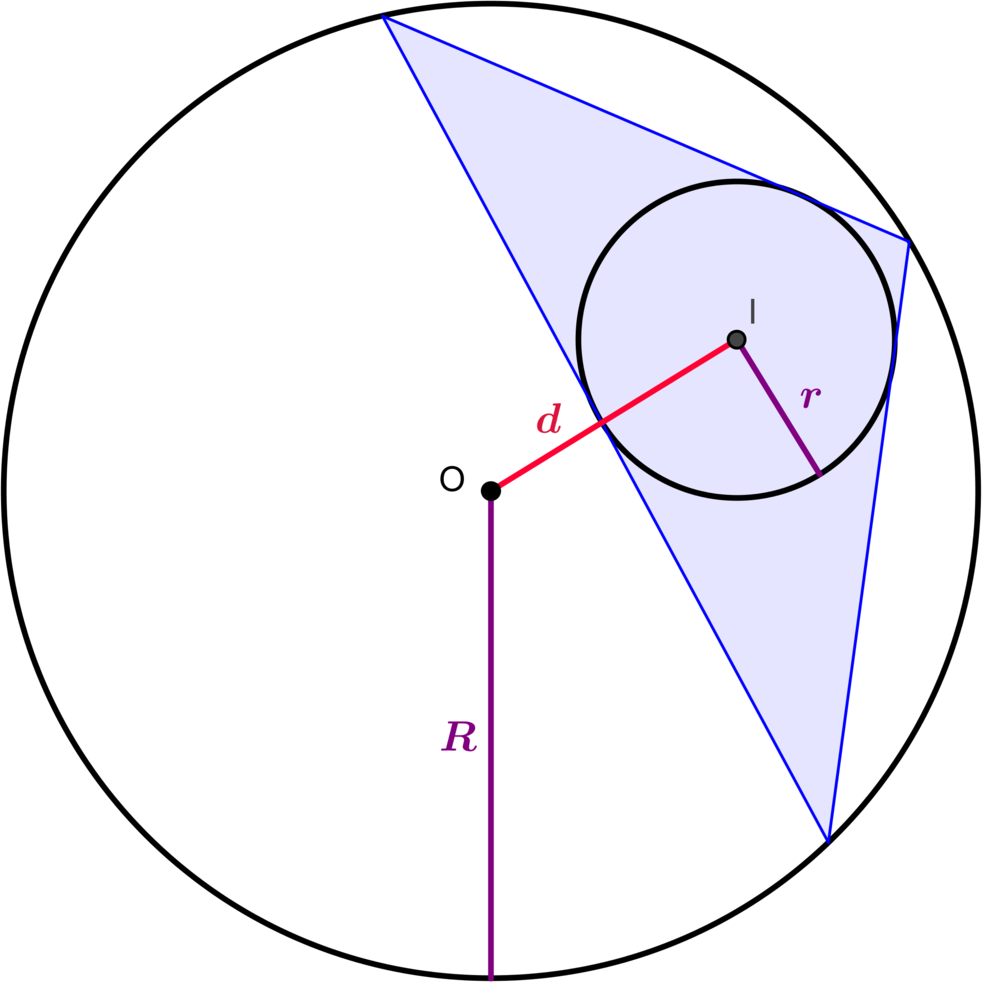
A similar puzzle in 2 dimensions was solved by Chapple in 1746 and Euler in 1765. Namely: suppose you have a circle contained in a larger circle. Suppose the radius of the large circle is R and the radius of the small one is r. Suppose the distance between their centers is d. Then you can fit a triangle between these two circles if and only if
d2≤R(R–2r)
Here is Milne’s picture of the situation:
In the comments on this blog, Greg Egan has proposed a generalized Grace–Danielsson inequality in n dimensions. More precisely, he has shown the following. Suppose we have a smaller ball of radius r inside a larger ball of radius R in Rn. Suppose the distance between the centers of these balls is d. Then we can fit an n-simplex inside the larger ball and outside the smaller one if
d2≤(R+(n−2)r)(R–nr),
where if the inequality is an equation the simplex may touch the surface of these balls. He conjectures that this sufficient condition is also necessary.
Egan writes:
Here’s a sketch of a result leading towards a higher-dimensional Grace–Danielsson inequality.
Given a small sphere with radius r in Rn, inside a larger sphere of radius R, and a distance of d between their centres, there’s an n-simplex we can try to construct that’s very symmetrical with respect to these spheres.
First, pick the point P on the small sphere that lies on the axis joining the centres of the spheres, and which is the furthest of the two such points from the larger sphere. The hyperplane tangent to the small sphere at P intersects the large sphere in an sphere of dimension one less—an (n−2)-sphere. Construct a regular (n−1)-simplex for which that (n−2)-sphere is its circumsphere.
Now, extend the (n−1)-simplex into an n-simplex by adding the point where the axis joining the centres of the original spheres intersects the large sphere, and which lies on the opposite side of the small sphere from P. By construction, one face of this n-simplex is tangent to the small sphere, and by symmetry if any other face avoids intersecting the small sphere, or is tangent to it, then the n-simplex will enclose the small sphere.
It’s not too hard to grind through the algebra and show that the condition that allows this is:
d2≤(R+(n−2)r)(R–nr)
So this condition is certainly sufficient for an n-simplex to fit between the nested spheres.
And then:
To flesh out my conjecture a little more, it’s helpful to start with an equation that is satisfied by the inradius r of an isosceles triangle with base 2b and height h:
b2(h−2r)–hr2=0
This is easy to prove from Pythagoras and similar triangles. The inradius is the radius of a circle that is tangent to all three sides of the triangle.
Now in the context of two nested spheres in Rn, the large one with radius R, the small one with radius r, and a distance of d between their centres, suppose we place a regular (n−1)-simplex tangent to the small sphere, with its centre at one of the points of intersection with the axis that runs between the centres of both spheres. If we choose a scale for this (n−1)-simplex so that its vertices lie on the large sphere, its circumradius will be given by the radius of the sphere of intersection between the large sphere and the hyperplane tangent to the small sphere, which is:
√R2−(r±d)2
Here the sign depends on which point of intersection with the axis we use as the point of tangency. The inradius of a regular (n−1)-simplex is smaller than the circumradius by a factor of n−1, so if we call that inradius b, we will have:
b2=R2−(r±d)2(n−1)2
Now, suppose we turn the regular (n−1)-simplex into an n-simplex by adding a point at the intersection of the axis and the large sphere that lies on the opposite side of the small sphere to the (n−1)-simplex. The “altitude” of this n-simplex measured from the (n−1)-simplex as its “base” will be given by:
h=R+(r±d)
We can construct an isosceles triangle by taking the centre of the regular (n−1)-simplex as the centre of the triangle’s base, the centre of any of the (n−2)-simplex faces of the regular (n−1)-simplex as an endpoint of the triangle’s base, and the added point we use to create the n-simplex as the triangle’s apex. This isosceles triangle with have a half-base of b and a height of h. What’s more, if every face of the n-simplex is tangent to the small sphere, then the radius of the small sphere, r, will be equal to the inradius of the isosceles triangle. So we have:
b2(h−2r)–hr2=0
It’s convenient to divide this through by h and multiply by (n−1)2, to obtain:
b2(n−1)2(h−2r)h–(n−1)2r2=0
Substituting in for b2 and h we get:
(R–(r±d))(R+(r±d)–2r)–(n−1)2r2=0
If we solve this for d2, we get:
d2=(R+(n−2)r)(R–nr)
So, this is the condition for an n-simplex with a regular (n−1)-simplex as its “base” to have all its faces tangent to the small sphere and all its vertices lying on the large sphere, given that we choose to make the “base” orthogonal to the axis running between the centres of the spheres.
For more details, see the comments.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




I thought I’d sketch some calculations I’ve been doing, which seem promising even though they haven’t yet yielded any rigorous proofs.
One lemma I’ve relied on is that if you can fit a simplex between a given ellipsoid and a sphere, you are free to choose a point P anywhere on the sphere and there will be a simplex that fits that has P as one of its vertices.
This animation is for a case where the Milne inequality becomes an equals sign, i.e. it is as tight a fit as possible, and yet we still have the freedom to put a vertex of the simplex anywhere on the sphere:
http://www.gregegan.net/SCIENCE/Simplex/SnugSimplices.gif
I haven’t written up a formal proof, but I think it should be easy to prove this by induction, starting with Poncelet’s Porism in two dimensions. In higher dimensions, imagine you have an n-simplex that fits, and if necessary you expand it into one whose vertices all lie on the sphere. While keeping one vertex V fixed and the hyperplane of the (n−1)-face opposite V fixed as well, you can intersect the cone of tangents to the ellipsoid from V into the hyperplane to get a lower-dimensional ellipsoid, and also intersect the hyperplane with the sphere, to create a new version of the nesting problem in dimension n−1. Assuming the lemma holds for n−1, the existence of the original (n−1)-face implies a whole family of other (n−1)-simplices that fit in the lower-dimensional problem, which include locations for one vertex anywhere at all on the lower-dimensional sphere. Any one of these can be turned back into a higher-dimensional simplex that fits in the original problem, simply by adjoining vertex V to them. And while this only gives us freedom to put a vertex anywhere on a particular lower-dimensional sphere, for each choice in that (n−2)-parameter family, we can follow up with a second transformation where we hold a different vertex fixed. That lets us place a vertex anywhere on the sphere.
As a corollary to this, if you can fit a simplex at all, it follows that you can nominate any unit vector u and find a simplex that fits and has u as the outwards normal to one of its faces.
What these results mean is that, without loss of generality, we can assume a convenient choice of u, such as an axis of the ellipsoid, even when the centre of the ellipsoid is displaced from the centre of the sphere by a generic vector. We can then assess the possibility of a fit in n dimensions by holding u fixed, putting a hyperplane tangent to the ellipsoid with u as its normal vector, then varying one candidate vertex, v, to see if the cone of tangents to the ellipsoid from v can ever intersect the hyperplane in a lower-dimensional ellipsoid that has room for a lower-dimensional simplex around it.
Using this approach, I’ve managed to derive the general 3D Milne condition from the 2D version. If you compute the 2D Milne quartic for the ellipse obtained from the tangent cone, it can be put into the form:
μ2(v)=a⋅v–b
where v is the vertex we’re free to vary, and a is a constant vector and b a positive constant scalar that depend only on the geometry of the problem and a choice of u as one of the ellipsoid axes. It’s not hard to see that μ2(v) can only be made positive for some choice of v with |v|2=R2 if:
R2|a|2–b2≥0
And R2|a|2–b2 factors into terms that include the 3D Milne quartic, μ3, regardless of which ellipsoid axis we chose for u.
I’m now trying to use the same kind of approach to obtain a generic condition for four dimensions, but it’s quite a bit harder, because even with u fixed μ3(v) isn’t linear in v.
The 2D Milne quartic for the ellipse obtained from a tangent cone can be put into the simple form:
μ2(v)=a⋅v–b
where v is the vertex we’re varying, subject to the constraint |v|=R. It’s easy to see that this will have its maximum when v is a multiple of a, and we can determine the relationship between a and b that allows that maximum to be at least zero.
But the 3D Milne quartic has an extra term, proportional to the square root of the determinant of the associated matrix. When we try to find the 4D condition by holding the hyperplane of one 3-face of the 4-simplex fixed and varying the vertex opposite, the form of the 3D Milne quartic we have to maximise is:
μ3(v)=a⋅v–b–√K((v−d)TM(v−d)–1)
where K is a constant, d is the centre of the 4D ellipsoid, and M is the matrix that defines the 4D ellipsoid through the equation:
(x−d)TM(x−d)=1
The most important goal is to identify the marginal case, where the maximum achieved by μ3(v) is zero. Because we’re imposing the constraint |v|=R, we don’t want the gradient of μ3(v) to be zero, but rather we want it to be parallel to the gradient of v⋅v, i.e. parallel to v itself. But if we also have the condition μ3(v)=0, we can multiply μ3(v) by any non-zero function f(v) at such a point, and the gradient of the product:
∇(f(v)μ3(v))=f(v)∇μ3(v)
will also be parallel to v. This allows us to multiply μ3(v) by:
a⋅v–b+√K((v−d)TM(v−d)–1)
to clear the square root, giving us the function:
G(v)=(a⋅v–b)2–K((v−d)TM(v−d)–1)
We want to find a simultaneous extremum and zero of G(v), still subject to the constraint |v|=R. This leads to an equation of the form:
2R2g⋅v+vTBv=0
where g is a vector and B a symmetric matrix defined in terms of our previous parameters. This equation describes an ellipsoid in 4D that will be tangent to the sphere |v|=R if the geometry of the original problem is a marginal case.
I don’t know a more efficient way to express the condition for an ellipsoid being tangent to a sphere than to describe both shapes projectively in 5D as homogeneous quadratic forms, say QE and QS, compute the determinant of a linear combination of the two:
D(α)=det
and then require that the degree-5 polynomial D(\alpha) have a double root. A polynomial has a double root when it shares a zero with its own derivative, so the condition we want can be expressed as a resultant, the determinant of a 9 \times 9 matrix in the coefficients of the polynomial D and its derivative.
So, the 4D condition ought to be a factor of that 9 \times 9 determinant (of a matrix whose entries are themselves high-degree polynomials, with hundred of terms, in the original parameters of the problem).
I’ve computed the full determinant with Mathematica, and even checked that it becomes zero in some expected cases (where the ellipsoid’s displacement from the centre of the sphere is aligned with one of its axes) … but so far Mathematica has been unable to factor the expression, after running for almost 24 hours!
I’ve still had no luck getting the completely general form for 4D, but I’ve managed to prove sufficiency for the case in n dimensions where the ellipsoid’s centre is displaced from the sphere’s centre in just two of the dimensions. For a vertex that lies in this plane and a hyperface opposite whose normal also lies in the plane, the tangent cone intersection is a lower-dimensional ellipsoid displaced from the centre of its lower-dimensional sphere in only a single dimension, and we already have a general formula for that case. This leads to a condition for the “planar displacement” case:
(d_1^2-(R+s_1+s_2-s_R) (R+s_1-s_2+s_R)) (d_1^2-(R-s_1-s_2-s_R) (R-s_1+s_2+s_R))+\\ (d_2^2-(R-s_1-s_2-s_R) (R+s_1-s_2+s_R)) (d_2^2-(R+s_1+s_2-s_R) (R-s_1+s_2+s_R))+\\ 2 d_1^2 d_2^2- (R-s_1-s_2-s_R)(R+s_1+s_2-s_R) (R+s_1-s_2+s_R) (R-s_1+s_2+s_R) \ge 0
Here s_R is the sum of all the semi-axes other than s_1 and s_2. In 2D, we set s_R=0 and this expression becomes the 2D Milne quartic.
I’ve been trying to pin down the general form for 4D by constructing homogeneous, suitably symmetric polynomials that, when specialised by setting some of the variables to zero, contain known cases as factors. Setting d_4 and s_4 to zero needs to give the 3D case, and setting d_3 and d_4 to zero needs to give the planar displacement case.
I found a 151-parameter family of degree 12 polynomials that specialise to give the correct 3D case and the 4D planar displacement case, and also the axially-aligned case which is a further specialisation of the planar case. But when specialised for the axially-aligned case, the degree 12 polynomials factored into four terms of the form:
(d_1^2 – (R \pm s_1 \pm s_2 \pm s_3 \pm s_4))
along with a quartic that depended on some of the parameters, but which could not be turned into a product of terms of the above form, for any choice of the parameters.
So I’m now looking for a family of degree 16, to see if I can get that kind of extra symmetry. I have a huge expression that I know must contain the 4D form as a factor, and though it’s too big to actually factorise I can at least check candidate factors.
I meant to write the factors of the axially aligned case as:
(d_1^2 – (R \pm s_1 \pm s_2 \pm s_3 \pm s_4)(R \pm s_1 \pm s_2 \pm s_3 \pm s_4))
I’ve now found a 1,423-parameter family of degree 16, and it does permit the axially aligned case to be written as a product of eight factors like this.
But this requirement doesn’t fix all the parameters, so I’m hoping to pin down the rest by imposing some further symmetries: requiring both the planar displacement and 3D specialisations to factor neatly into four quartics that differ only in choices of signs for the s_i.
I’ve finally managed to isolate the 4D formula, as a degree 16 polynomial in the semi-axes and centre offset coordinates! To pin it down, I started with a generic degree 16 polynomial that was symmetric under permutations of the indices for d_i and s_i, and then I found some coefficients by requiring that the polynomial contained all the known cases as factors when I specialised it. That still wasn’t enough, though, so to find the remaining coefficients I repeatedly substituted random integers for all but one of the variables in the discriminant that was too huge to factor, leaving a polynomial in a single variable that could be factored. Requiring my candidate polynomial with the same substitutions to agree with one factor of the discriminant gave equations for the unknown coefficients … and repeating the process a few hundred times after the coefficients were known verified the solution.
There are 12,870 terms in the polynomial, so it’s not very enlightening as it stands, but I’m hoping to find a way to rewrite it in terms of traces, determinants, etc.
I’ve just realised that the degree-16 polynomial I found suffers from a major flaw. I believe that the region where it’s positive includes all cases where a nested simplex is possible, but there are also spurious extra regions where it becomes positive where this is not the case.
The Milne quartic could also give “false positives”, but only when the centre of the ellipsoid lay outside the sphere. But with this degree-16 polynomial, the false positives appear inside the sphere.
I suspect this means that it’s impossible to find a single polynomial expression whose sign being positive is necessary and sufficient for the existence of a nested simplex, for an ellipsoid at an arbitrary location inside the sphere, in four or more dimensions.
That’s disappointing, but there’s still the simple formula for the axis-aligned case in n dimensions, so maybe I can think of another way to prove that that’s necessary as well as sufficient.
I’m going to try one more thing: seeing if I can do the induction on a non-polynomial expression that identifies the upper limit for d^2, which ought to be a well-defined single-valued function. For example, Milne’s inequality:
d^4 – 2 u d^2 + q \ge 0
is easily converted to an inequality with no false positives at all, just by explicitly choosing the lower root of the quadratic in d^2:
d^2 \le u – \sqrt{u^2 – q}
Here, q is entirely independent of the displacement vector d, while u depends on a unit vector \hat{d} in the direction of the displacement.
My instinct up until now has been to try to clear as many square roots as possible to make the calculations simpler, but now that I’ve realised the downside of that I should try the opposite approach!