Discriminant of the Icosahedral Group
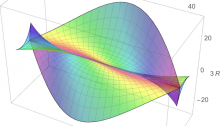
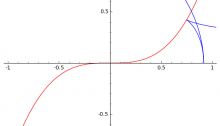
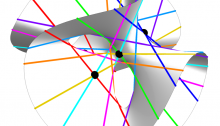
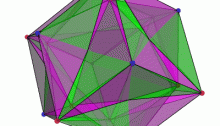
This image, created by Greg Egan, shows the ‘discriminant’ of the symmetry group of the icosahedron. This group acts as linear transformations of \(\mathbb{R}^3\) and thus also \(\mathbb{C}^3\). By a theorem of Chevalley, the space of orbits of this group action is again isomorphic to \(\mathbb{C}^3\). Each point in the surface shown here corresponds to a ‘nongeneric’ orbit: an orbit with fewer than the maximal number of points. More precisely, the space of nongeneric orbits forms a complex surface in \(\mathbb{C}^3\), called the discriminant, whose intersection with \(\mathbb{R}^3\) is shown here.