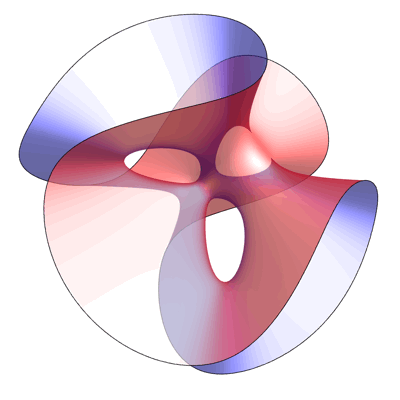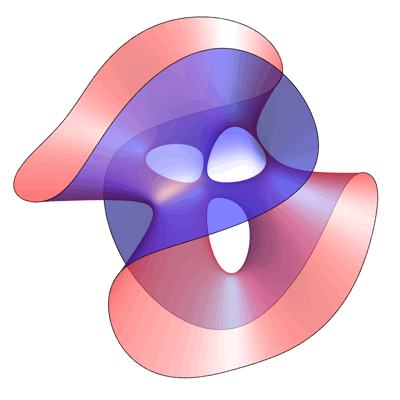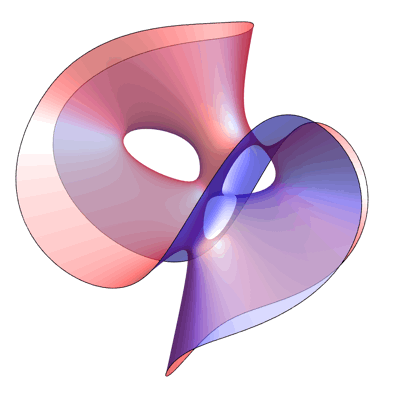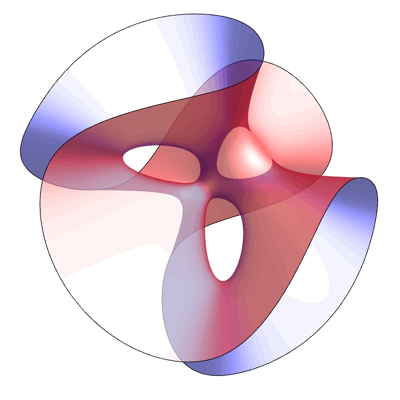
Clebsch Surface – Greg Egan
This is an image of the Clebsch surface, created by Greg Egan. As explained in a previous post here, the Clebsch surface owes its fame to the fact that while all smooth cubic surfaces defined over the complex numbers contain 27 lines, for this particular example all the lines are real, and thus visible to the eye:
• 27 lines on a cubic surface.
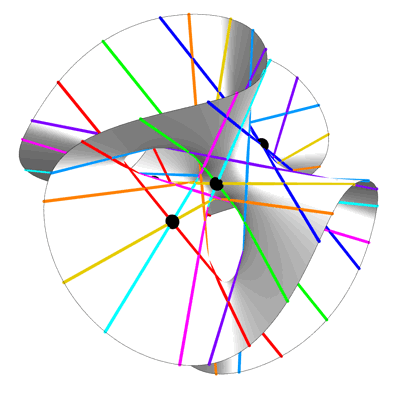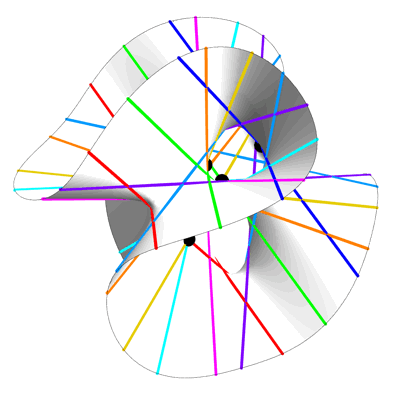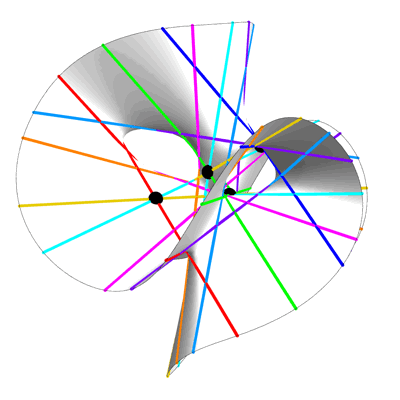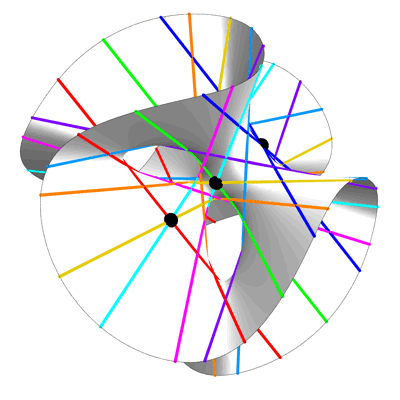
27 Lines on a Cubic Surface – Greg Egan
The equation of the Clebsch cubic is simple and elegant when we regard it as a projective variety, but this view of it in R3 is given by the following more complicated equation:
81(x3+y3+z3)–189(x2y+x2z+xy2+xz2+y2z+yz2)+54xyz+126(xy+xz+yz)–9(x2+y2+z2)–9(x+y+z)+1=0.
This equation is invariant under permutations of the variables x,y,z. This gives the picture above its 3-fold symmetry.
A point where 3 lines on a cubic surface meet is called an Eckardt point. The Clebsch surface is the only smooth cubic surface with 10 Eckardt points. In the view above, 3 of the Eckardt points are invisible, since they are at the plane at infinity.
Here are two images, each showing part of the Clebsch surface. In each image, Egan has sliced the surface with a plane, and shown only the portion of the surface on one side of this plane. The Eckardt points that lie exactly on the cutting plane are colored gray, while the remainder are colored black:

Half of the Clebsch Surface – Greg Egan
In the picture above, he cut through a plane that contains the axis of symmetry and one of the blue lines. Note that this is not a plane of mirror symmetry.
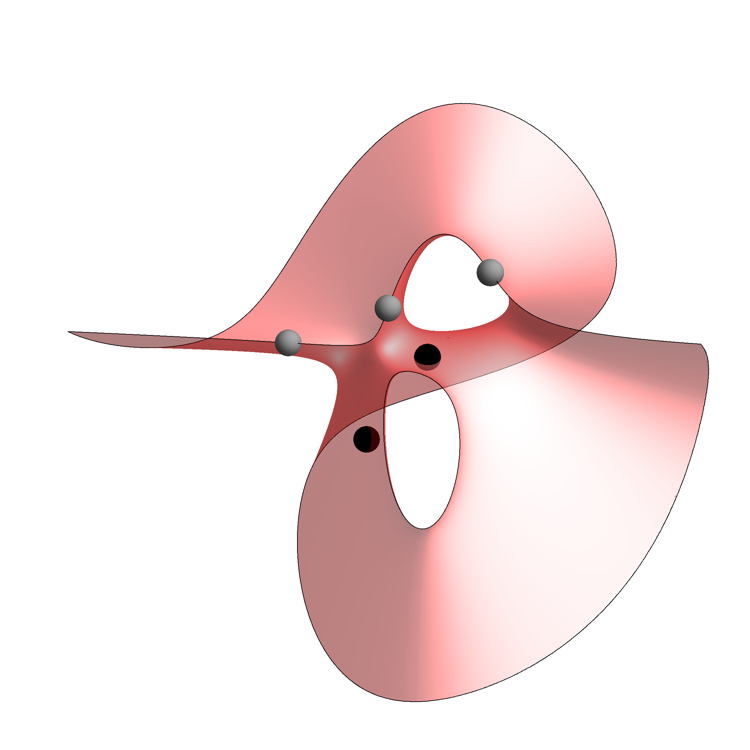
Another Half of the Clebsch Surface – Greg Egan
Given a point p in a 2-dimensional complex algebraic variety X one can build a new variety in which the point p is inflated or ‘blown up’ to a projective line. The idea is that different points of CP1 correspond to different lines through the origin in the tangent space of p. So, as we approach the original point p in different directions, in the new variety we approach different points of CP1. This procedure creates a new variety Xp equipped with an algebraic map
π:Xp→X
that is surjective, with the inverse image of p being a copy of CP1.
Every smooth cubic surface can be obtained by blowing up the projective plane CP2 at 6 points. Conversely, suppose we have 6 points in CP2 such that no 3 lie on a line and not all 6 lie on a conic. Then if we blow up CP2 at all 6 of these points, we get a surface isomorphic to a smooth cubic. Thus, the Clebsch cubic can be obtained by blowing up CP2 at 6 suitably chosen points.
In 1873, Felix Klein described these points as follows. If the projective plane CP2 is identified with the set of lines through the origin in a copy of C3 containing a copy of R3 that in turn contains an icosahedron centered at the origin, then the 6 points correspond to the 6 lines through the icosahedron’s 12 vertices! The Eckardt points correspond to the 10 lines through the centers of the 20 faces.
For this reason, the Clebsch surface is also called Klein’s icosahedral cubic surface. This construction shows that its group of symmetries is larger than S3, since symmetries of the icosahedron also act as symmetries of this surface. Here by ‘symmetry’ we mean a biholomorphic transformation: a complex-analytic map with complex-analytic inverse.
In fact, the symmetry group of the Clebsch surface is as large as possible for a cubic surface: it is S5. The presence of these symmetries becomes obvious if we use the description we began with in our previous post: the Clebsch surface is the projective variety defined by the homogeneous equations
x0+x1+x2+x3+x4=0,x30+x31+x32+x33+x34=0.
The group S5 acts by permuting the 5 coordinates.
Many old universities have nice plaster models of the Clebsch surface. For a nice discussion of the model at Oxford, with more on the mathematics of this surface and its relation to the affine Dynkin diagram of E6, see:
• Mathematical Institute, The University of Oxford, The Clebsch diagonal surface.
You can buy a model of the surface here:
• MOLabs, Cubic surfaces.
This is Klein’s paper on the Clebsch surface:
• Felix Klein, Ueber Flächen dritter Ordnung, Mathematische Annalen 6 (1873), 551–581.
and this is the paper where Clebsch introduced the surface:
• Alfred Clebsch, Ueber die Anwendung der quadratischen Substitution auf die Gleichungen 5ten Grades und die geometrische Theorie des ebenen Fünfseits, Mathematische Annalen 4 (1871), 2847–345.
This is a nice introduction to blowing up:
• Marc Brodmann, Blowing up!
and here is a more advanced one:
• Herwig Hauser, The Hironaka theorem on resolution of singularities (or: a proof we always wanted to understand), Bull. Amer. Math. Soc. 40 (2003), 323–403.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!



