27 Lines on a Cubic Surface – Greg Egan
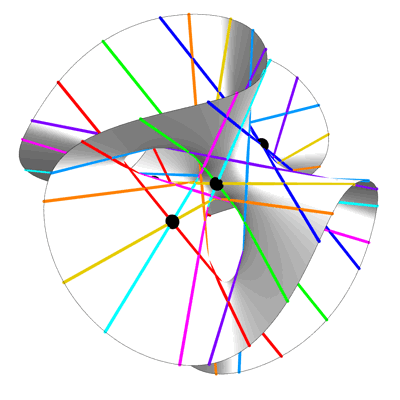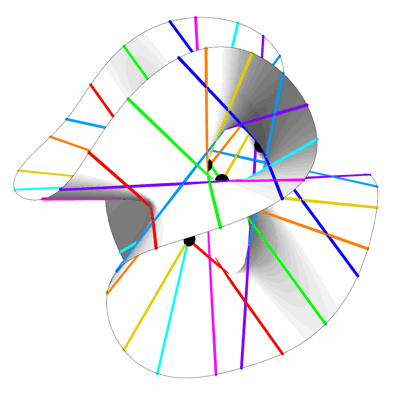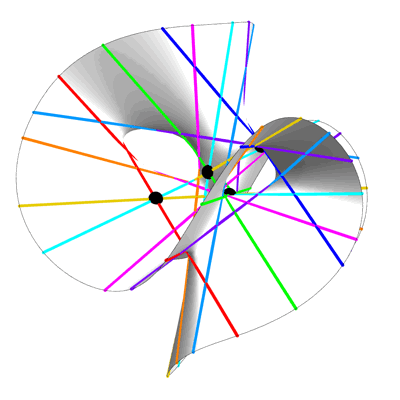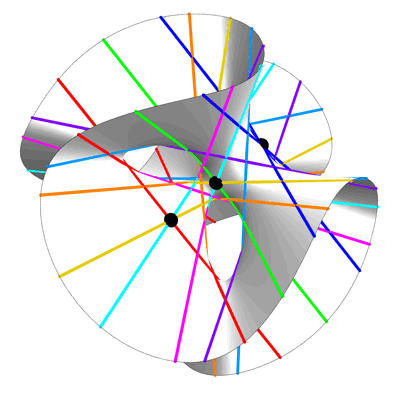
This animation by Greg Egan shows 27 lines on a surface defined by cubic equations: the Clebsch surface. It illustrates a remarkable fact: any smooth cubic surface contains 27 lines.
In its most symmetrical presentation, the Clebsch surface is defined by the equations
x0+x1+x2+x3+x4=0x30+x31+x32+x33+x34=0
where x0,…,x4 are complex variables. These two equations pick out a subset S⊂C5 with complex dimension 3. Note that if (x0,…,x4)∈C5 is a solution, so is any multiple (cx0,…,cx4). We may thus projectivize S, treating any solution as ‘the same’ as any multiple of that solution. The result is a submanifold X of the complex projective space CP4. This has complex dimension 2, and it is a smooth algebraic variety, so we call it a smooth complex surface.
We can also eliminate the variable x0 in the above equations, and define the Clebsch surface starting from the single homogeneous cubic equation
x31+x32+x33+x34=(x1+x2+x3+x4)3
in variables x1,…,x4. Projectivizing this, we get a smooth complex surface in CP3. Since it is defined by a homogeneous cubic equation, it is called a smooth cubic surface.
The Clebsch surface illustrates a remarkable result in algebraic geometry, the Cayley–Salmon theorem, which states that any smooth cubic surface contains 27 straight lines. No matter how one goes about it, the proof of this theorem is nontrivial. For a very helpful introduction to the main ideas, see:
• Jack Huizenga, Algebraic geometry: why are there exactly 27 straight lines on a smooth cubic surface?, Quora.
For the Clebsch surface, the 27 lines are easiest to describe as 2-dimensional subspaces of C5. We first define
ζ=e2πi/5.
The 27 2-dimensional subspaces are:
• The 15 subspaces obtained from the one containing (1,−1,0,0,0) and (0,0,1,−1,0) by permuting the 5 coordinates in an arbitrary way.
• The 12 subspaces obtained from the one containing (1,ζ,ζ2,ζ3,ζ4) and (1,ζ−1,ζ−2,ζ−3,ζ−4) by permuting the 5 coordinates in an arbitrary way.
It is easy to check that all these subspaces lie in S⊂C5.
The special virtue of the Clebsch surface is that all 27 lines are visible even when we restrict attention to real solutions, obtaining an ordinary 2-dimensional real surface that we can draw, rather than a complex surface.
To obtain the above picture, Greg Egan first considered the space of real solutions of
x31+x32+x33+x34=(x1+x2+x3+x4)3.
He then projectivized this space of solutions, obtaining a surface in the real projective space RP3. To draw the surface in R3 he then picked a certain plane in RP3 to be the ‘plane at infinity’. Following Bruce Hunt, he chose
x0+x1+x2+4x3=0.
The resulting surface in R3 has the equation
81(x3+y3+z3)–189(x2y+x2z+xy2+xz2+y2z+yz2)+54xyz+126(xy+xz+yz)–9(x2+y2+z2)–9(x+y+z)+1=0.
This surface omits some points in the Clebsch cubic, which have become ‘points at infinity’.
The picture above is a rotating view of this surface, the 27 lines on this surface, and 7 of the 10 Eckardt points: points where 3 lines meet. The remaining 3 Eckardt points are at infinity.
He drew the lines in a way that makes them easy to count: there are 3 lines of each of 9 colors, with each triple having an order-3 rotational symmetry. The three Eckardt points at infinity can also be easily described in terms of this image: they are the 3 points at infinity where parallel red, green and blue lines meet.
Here are some still views of the Clebsch cubic:
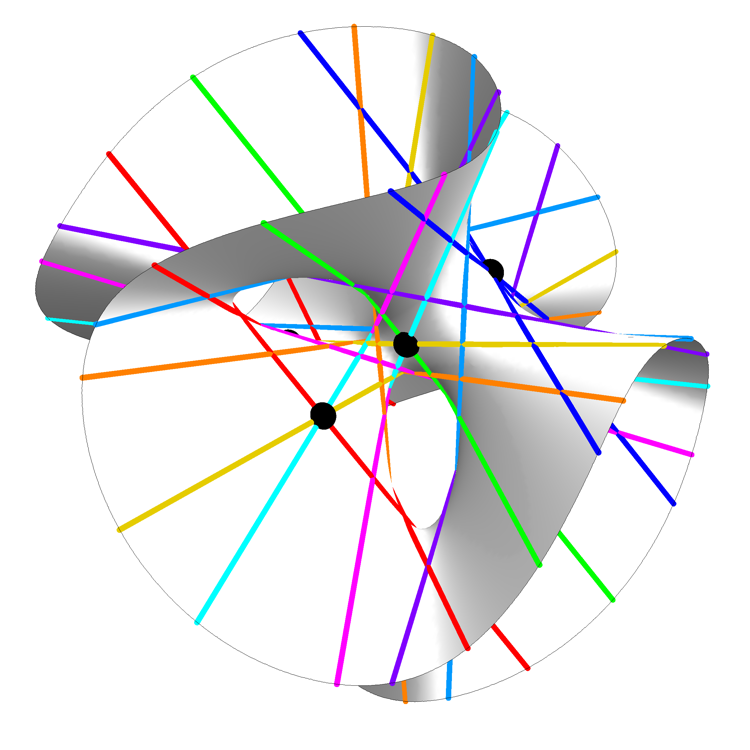
Clebsch Cubic (Still View) – Greg Egan
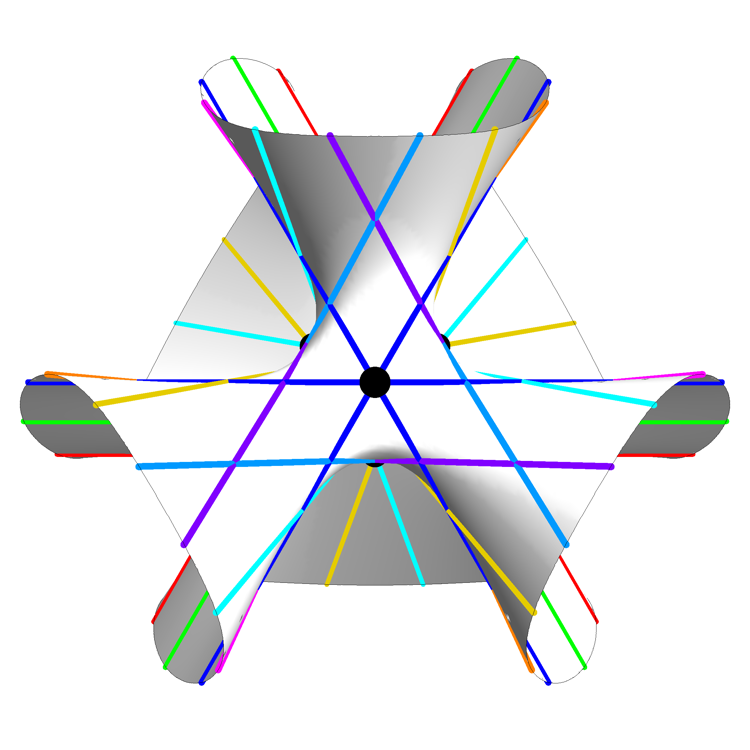
Clebsch Cubic (Symmetrical Still View) – Greg Egan
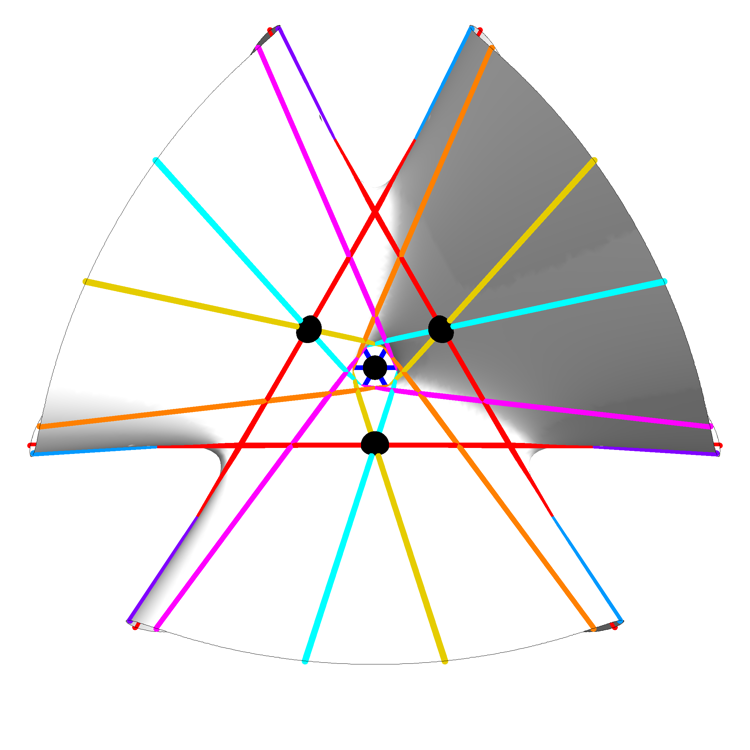
Clebsch Cubic (Still View Showing Hole) – Greg Egan
The last view shows a hole in the Clebsch cubic that is invisible in the other views!
Bruce Hunt has given a detailed explanation of the Clebsch cubic surface, invaluable for anyone wanting to understand this and also the beautiful combinatorics surrounding the 27 lines on any smooth cubic:
• Bruce Hunt, The Geometry of Some Special Arithmetic Quotients, Chapter 4: The 27 lines on a cubic surface, Springer Lecture Notes in Mathematics 1637, Springer, Berlin, 1996.
The 27 lines on the cubic are also connected to the 27-dimensional exceptional Jordan algebra, which (along with its dual) provides the smallest nontrivial representation of the exceptional Lie group E6. This is part of a much larger story discussed here:
• Laurent Manivel, Configurations of lines and models of Lie algebras, Journal of Algebra 304 (2006), 457–486.
For more on the Clebsch surface see this other post:
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!




Very nice!
Small point: the link to Jack Huizenga’s Quora answer points to the wrong place.
As explained at https://en.wikipedia.org/wiki/Clebsch_surface, there is another beautiful construction of the Clebsch surface obtained from the icosahedron. Do you know if it’s possible to “see” the icosahedron in these pictures?
Sorry to take so long to reply: I somehow missed this comment.
I don’t know how to see the icosahedron lurking in the Clebsch surface, but I describe that construction here:
• [Clebsch surface](http://blogs.ams.org/visualinsight/2016/03/01/clebsch-surface/).
Great post!
The Quora link goes to Wikipedia, the actual link should be https://www.quora.com/Algebraic-Geometry/Why-are-there-exactly-27-straight-lines-on-a-smooth-cubic-surface/answer/Jack-Huizenga
Yes, I’ll fix that. Thanks.
Ever since I first saw this post I’ve been wanting to make an interactive version with Three.js, and here it is:
27 Lines on a Cubic Surface
I find a fully interactive version much more interesting.
Cool, I’ll check it out! Thanks, and sorry for taking so long to moderate this!