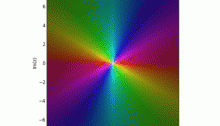
The Weierstrass elliptic function is built up as a sum of terms, one for each point in a lattice in the complex plane. Each term has a pole at one lattice point. The picture here shows the very first term, namely $1/z^2$. That’s why it’s bright in the middle and the colors go twice around the color wheel as you go around. If you continue reading, you’ll see a movie made by David Chudzicki where further terms are added one at a time!
Suppose we inscribe a regular pentagon, a regular decagon, and a regular hexagon in circles of the same radius. If we denote the respective edge lengths of these polygons by $P$, $D$ and $H$, then these lengths obey $P^2=D^2+H^2$. So, the edges of a pentagon, decagon and hexagon of identical radii can fit together to form a right triangle! Recently Greg Egan gave a nice proof using the icosahedron.
This is a truncated 4-dimensional cube, drawn in a curved style by Jos Leys. You can take an ordinary 3-dimensional cube, cut off its corners and get a truncated cube. Similarly, you can take a 4-dimensional cube, cut off its corners, and get a 4-dimensional uniform polytope with $2 \times 4 = 8$ truncated cubes as faces and $2^4 = 16$ tetrahedral faces! It’s called the truncated 4-cube.
A deltoid is a curve formed by rolling a circle inside a circle whose radius is 3 times larger. Similarly, an astroid is a curve formed by rolling a circle inside a circle whose radius is 4 times larger. The picture here, drawn by Greg Egan, shows a deltoid rolling inside an astroid. It fits in a perfectly snug way!
This image, drawn by Xah Lee, shows a deltoid and its catacaustic. The deltoid is the curve traced by a point on the perimeter of a circle that is rolling inside a fixed circle whose radius is three times as big. It’s called a deltoid because it looks a bit like the Greek letter delta: $\Delta$. The catacaustic of a curve in the plane is the envelope of rays emitted from some source and reflected off that curve.
This is the Enneper surface, as drawn by Greg Egan using Mathematica. It’s a minimal surface, meaning one that necessarily gets more area if you warp any small patch of it. A soap film will make a minimal surface if it doesn’t enclose any air. But the Enneper surface intersects itself: it’s immersed in 3d space, but not embedded. So, you can’t make it with soapy water!
This picture, drawn by Elias Wegert, uses colors to show the phase $f/|f|$ of the complex function
$$f(z) = \prod_{k=1}^5 \exp\left(\frac{z+\omega^k}{z-\omega^k}\right)$$
where $\omega$ is a nontrivial fifth root of unity. This is an ‘atomic singular inner function’. To understand what that means, it helps to start with some complex analysis.
This image, drawn by Greg Egan, shows a cardioid and its catacaustic. The cardioid is a heart-shaped curve traced by a point on the perimeter of a circle that is rolling around a fixed circle of the same radius. The catacaustic of a curve in the plane is the envelope of rays emitted from some…
A 3-dimensional honeycomb is a way of filling 3d space with polyhedra. It’s the 3-dimensional analogue of a tiiling of the plane. However, not only can we have honeycombs in Euclidean space, we can also have them in hyperbolic space. The {6,3,3} honeycomb lives in hyperbolic space.
This is a picture of the algebraic numbers in the complex plane, made by David Moore based on earlier work by Stephen J. Brooks. Algebraic numbers are roots of polynomials with integer coefficients. In this picture the color indicates the degree of the polynomial.
Notices of the AMS · Bulletin of the AMS
American Mathematical Society · 201 Charles Street Providence, Rhode Island 02904-2213 · 401-455-4000 or 800-321-4267
© Copyright , American Mathematical Society · Privacy Statement