Astroid as Catacaustic of Deltoid – Xah Lee

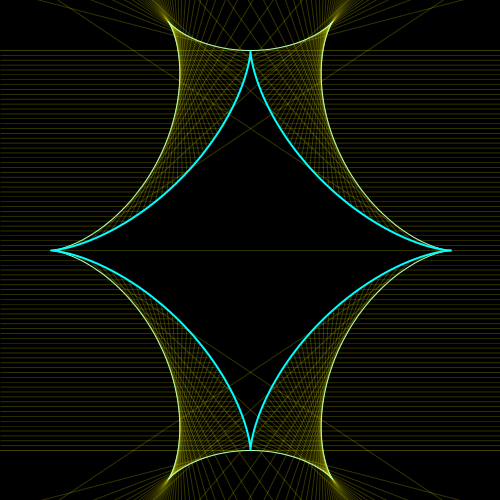
This image, drawn by Xah Lee, shows a deltoid and its catacaustic.

The deltoid is the curve traced by a point on the perimeter of a circle that is rolling inside a fixed circle whose radius is three times as big. It’s called a deltoid because it looks a bit like the Greek letter delta: $\Delta$.

The catacaustic of a curve in the plane is the envelope of rays emitted from some source and reflected off that curve.

If we shine parallel rays at one corner of the deltoid, the resulting catacaustic is called the astroid. This is the curve traced by a point on the perimeter of a circle that is rolling inside a fixed circle whose radius is four times as big! It’s called an astroid because it looks like a star.

Does this fact generalize? If we take a circle and roll it inside a circle whose radius is $n$ times as big, and trace out the motion of one point, we get a curve called the hypocycloid with $n$ cusps. Is the catacaustic of a hypocycloid with $n$ cusps a hypocycloid with $n+1$ cusps?

No: according to Egan the catacaustic of an astroid is not a hypocycloid. For an astroid with cusps on the coordinate axes and a light source at $(-\infty,0)$, the catacaustic has 6 cusps, and it looks like this:

Catacaustic of an Astroid – Greg Egan

It has this parametric form, up to scale:

$$ (\cos(3t) + 3 (4 \cos(t)+ \cos(5t)), 2 \sin(2t) (\cos(t)-9 \cos(3t)) – 4 \cos(2t) (\sin(t)-3 \sin(3t)))) $$

Xah Lee has a great website devoted to curves:

• Xah Lee, Visual dictionary of special plane curves.

Also see Egan’s page on catacaustics:

• Greg Egan, Catacaustics, resultants and kissing conics.

For more on deltoids, astroids and other hypocycloids, see these:

• John Baez, Rolling circles and balls.

• Deltoid rolling inside astroid, Visual Insight.

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!