{6,3,3} Honeycomb in Upper Half Space – Roice Nelson
A 3-dimensional honeycomb is a way of filling 3d space with polyhedra. It’s the 3-dimensional analogue of a tiling of the plane.
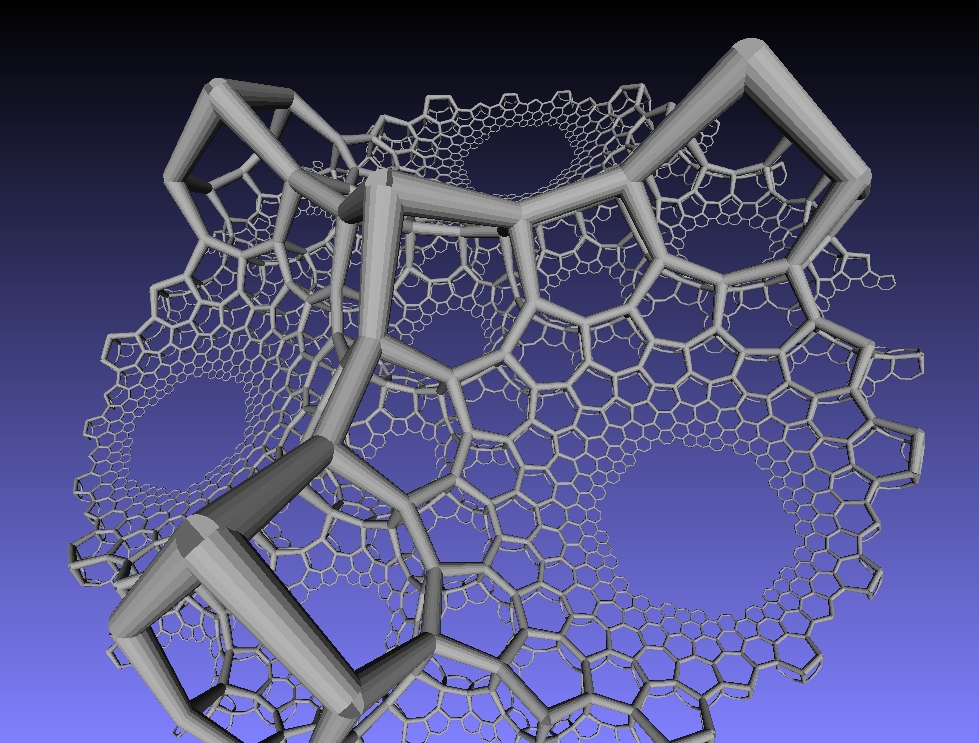
However, besides honeycombs in Euclidean space, we can also have honeycombs in hyperbolic space, which is a 3-dimensional Riemannian manifold with constant negative curvature. The {6,3,3} honeycomb lives in hyperbolic space. Here Roice Nelson has drawn it in the upper half space model of hyperbolic space, which is the 3d analogue of Poincaré’s famous upper half-plane model of the hyperbolic plane. As usual, you can click the image for a better view!
The {6,3,3} honeycomb is also called the hexagonal tiling honeycomb. The reason is that three hexagonal tilings of the plane meet at any edge of this honeycomb. This fact is recorded in the notation {6,3,3}, which is an example of a Schläfli symbol. The Schläfli symbol is defined in a recursive way. The symbol for the hexagon is {6}. The symbol for the hexagonal tiling of the plane is {6,3} because 3 hexagons meet at each vertex. Similarly, the symbol for the hexagonal tiling honeycomb is {6,3,3} because 3 hexagonal tilings meet along each edge.
The {6,3,3} honeycomb is one of 15 regular honeycombs in hyperbolic space. For a complete list, with links to pictures, see:
• Tesselations of hyperbolic 3-space, Wikipedia.
Roice Nelson is a software developer with a passion for exploring mathematics through visualization:
• Roice.
Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!
