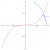
A deltoid is a curve formed by rolling a circle inside a circle whose radius is 3 times larger. Similarly, an astroid is a curve formed by rolling a circle inside a circle whose radius is 4 times larger. The picture here, drawn by Greg Egan, shows a deltoid moving inside an astroid. Note that it fits in a perfectly snug way!

It looks like it’s rolling. However, it doesn’t truly ‘roll’ in the true sense of classical mechanics—-it slides a bit as it rolls.

This pattern continues. The hypocycloid with $n$ cusps is the curve formed by rolling a circle inside a circle whose radius is $n$ times larger. A hypocycloid with $n$ cusps moves snugly inside a hypocycloid with $n+1$ cusps.

For another relation between the deltoid and astroid, see:

• Astroid as catacaustic of deltoid, Visual Insight.

This pattern does not continue.

To see why the hypocycloid with $n$ cusps moves snugly inside a hypocycloid with $n+1$ cusps, it helps to think about a related surprise. Recall that the special unitary group $\mathrm{SU}(n)$ consists of $n \times n$ unitary matrices with determinant 1. In fact, the set of complex numbers that are the trace of some matrix in the group $\mathrm{SU}(n)$ is filled-in hypocycloid with $n$ cusps! This is discussed here:

• N. Kaiser, Mean eigenvalues for simple, simply connected, compact Lie groups.

But here is a fairly self-contained proof put together by Greg Egan, with some help from Shanthanu Bhardwaj and Aaron Wolbach.

If you have a matrix in $\mathrm{SU}(n+1)$, its $n+1$ eigenvalues can be any unit complex numbers that multiply to 1, and its trace is the sum of these numbers. We can take $n$ of them to be $e^{i \theta}$, and then the remaining one has to be $e^{-i n \theta}$. Then their sum is

$$ n e^{i \theta} + e^{-i n \theta}. $$

But this is also the curve traced out by a small circle of radius 1 rolling inside a big circle of radius $n+1$. Why? As it rolls, the small circle’s center moves around a circle of radius $n$, tracing out the curve $n e^{i \theta}$. But as it rolls, the small circle turns in the opposite direction at an angular velocity that’s $n$ times higher. This gives the term $e^{-i n \theta}$.

In short, we have seen that

$$ H_{n+1} = \{ n e^{i \theta} + e^{-i n \theta} : 0 \le \theta \le 2 \pi \} $$

is a hypocycloid with $n+1$ cusps, and if we define

$$\mathrm{tr}(\mathrm{SU}(n+1)) = \{ \mathrm{tr}(g) : g \in \mathrm{SU}(n+1) \} $$

then

$$ H_{n+1} \subseteq \mathrm{tr}(\mathrm{SU}(n+1)) .$$

In fact, the hypocycloid $H_{n+1}$ is precisely the boundary of $\mathrm{tr}(\mathrm{SU}(n+1))$. To show this, note that the eigenvalues of any element of $\mathrm{SU}(n+1)$ can be written as

$$ e^{i\phi_1} , \; \dots, \; e^{i\phi_{n}} , \; e^{-i(\phi_1+\phi_2+ \cdots +\phi_{n})} $$

so its trace is

$$ e^{i\phi_1} + \cdots + e^{i\phi_{n}} + e^{-i(\phi_1+\phi_2+ \cdots +\phi_{n})} $$

where the angles $\phi_i$ are arbitrary. When all the $\phi_i$ equal the same angle $\theta$, the trace gives a point in the hypocycloid $H_{n+1}$. But if we compute the derivative of the trace with respect to any angle $\phi_i$ at a point where they’re all equal, the derivative is always tangent to this hypocycloid: it’s just $\frac{1}{n-1}$ times the derivative of

$$ n e^{i \theta} + e^{-i n \theta}$$

with respect to $\theta$. Except at the cusps, some neighborhood of the tangent line lies in the interior of the filled hypocycloid, so no change in the $\phi_i$ can take you out of it. And at the cusps, moving along the tangent out of the hypocycloid would take you out of the disk of radius $n$, which is forbidden by the triangle inequality.

Furthermore, any point inside the hypocycloid $H_{n+1}$ is an element of $\mathrm{tr}(\mathrm{SU}(n+1))$. To see this, note that $\mathrm{SU}(n+1)$ is simply connected, and thus so is its image under the continuous map

$$ \mathrm{tr} \colon \mathrm{SU}(n+1) \to \mathbb{C} .$$

Since its image includes the hypocycloid $H_{n+1}$, which bounds a set homeomorphic to a disk, its image must include this whole set. (Here we use a fact from topology, that a subset of a disk containing the boundary but missing some point in the interior cannot be simply connected.)

In summary, $\mathrm{tr}(\mathrm{SU}(n+1))$ is precisely the closed set in the plane bounded by hypocycloid $H_{n+1}$. We can use this to see that a hypocycloid with $n$ cusps rolls snugly inside a hypocycloid with $n+1$ cusps. Recall that the eigenvalues of a matrix in $\mathrm{SU}(n)$ are of the form

$$ e^{i\phi_1}, \; \dots , \; e^{i\phi_{n-1}}, \; e^{-i(\phi_1+\phi_2+…+\phi_{n-1})} $$

where the angles $\phi_i$ are arbitrary. On the other hand, the eigenvalues of any element of $\mathrm{SU}(n+1)$ can be written as

$$ e^{i\theta}e^{i\phi_1}, \; \dots , \; e^{i\theta}e^{i\phi_{n-1}}, \;e^{i\theta}e^{-i(\phi_1+\phi_2+…+\phi_{n-1})}, e^{-in\theta} $$

where the angles $\phi_i$ and $\theta$ are arbitrary. Thus we have

$$ \mathrm{tr}(\mathrm{SU}(n+1)) = \bigcup_{0 \le \theta \le \pi} e^{i\theta} \mathrm{tr}(\mathrm{SU}(n)) + e^{-in\theta} $$

As $\theta$ ranges from $0$ to $2\pi$, this gives a filled-in hypocycloid with $n$ cusps moving snugly inside one with $n+1$ cusps!

Egan’s picture above illustrates the case $n = 2$. The circling red dot shows what happens as $\theta$ changes. Each of the colored lines shows what happens when we vary $\phi_1$, while the progression from line to line sweeping out a filled-in deltoid is due to varying $\phi_2$.

For Egan’s movie of the case $n = 3$, and also some movies of nested hypocycloids, each one moving in the next, see:

• John Baez, Rolling Hypocycloids, Azimuth.

For the discussion in which this proof was put together, see the comments here:

• John Baez, Rolling Circles and Balls (Part 3), Azimuth.

---

Visual Insight is a place to share striking images that help explain advanced topics in mathematics. I’m always looking for truly beautiful images, so if you know about one, please drop a comment here and let me know!